Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Đặt z = x + y i , x , y ∈ ℝ .
Ta có z - 3 i - 1 = ( x - 1 ) + ( y - 3 ) i = x - 1 2 + y - 3 2
Do đó 3 ≤ z - 3 i + 1 ≤ 5 ⇔ 9 ≤ x - 1 2 + y - 3 2 ≤ 25
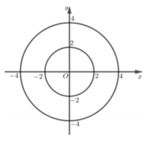
Suy ra tập hợp các điểm biểu diễn của z là hình phẳng nằm trong đường tròn tâm I(1;3) bán kính R = 5 đồng thời nằm ngoài đường tròn tâm I(1;3) bán kính r = 3.
Diện tích của hình phẳng đó (phần tô màu) là S = π . 5 2 - π . 3 2 = 16 π (đvdt).

Phương pháp:
Sử dụng phương pháp hình học: Tìm tập hợp các điểm biểu diễn số phức z, w và tính toán.
Cách giải:



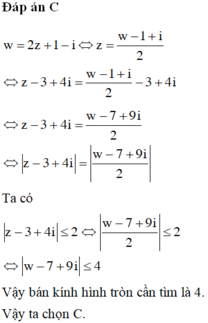


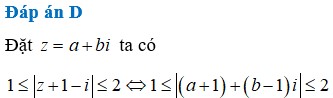
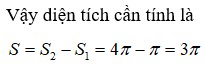
Đáp án D.
Gọi M là điểm biểu diễn của số phức z. Xét điểm A − 1 ; 3 thì theo điều kiện, ta có: 3 ≤ z − 3 i + 1 ≤ 5 ⇔ 3 ≤ A M ≤ 5. Vậy tập hợp các điểm biểu diễn z là phần hình phẳng nằm giữa 2 đường tròn tâm A, bán kính lần lượt là 3 và 5
⇒ S = π 5 2 − 3 3 = 16 π .