K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 2 2023
3/10>3/15
3/11>3/15
3/12>3/15
3/13>3/15
3/14>3/15
=>S>3/15*5=15/15=1
3/11<3/10
3/12<3/10
3/13<3/10
3/14<3/10
=>3/11+3/12+3/13+3/14+3/10<3/10*5=15/10=3/2<2
=>1<S<2
YS
10 tháng 3 2016
S = 3/10 + 3/11 + 3/12 + 3/13 + 3/14 > 3/15 + 3/15 + 3/15 + 3/15 + 3/15 = 15/15 = 1
=> 1 < S = 3/10 + 3/11 + 3/12 + 3/13 + 3/14 < 3/10 + 3/10 + 3/10 + 3/10 + 3/10 = 20/10 = 2
=> 1 < S < 2 (điều cần chứng minh)
DD
Đoàn Đức Hà
Giáo viên
20 tháng 8 2021
\(\frac{3}{10}+\frac{3}{11}+\frac{3}{12}+\frac{3}{13}+\frac{3}{14}>\frac{3}{15}+\frac{3}{15}+\frac{3}{15}+\frac{3}{15}+\frac{3}{15}=\frac{15}{15}=1\)
\(\frac{3}{10}+\frac{3}{11}+\frac{3}{12}+\frac{3}{13}+\frac{3}{14}< \frac{3}{9}+\frac{3}{9}+\frac{3}{9}+\frac{3}{9}+\frac{3}{9}=\frac{15}{9}< \frac{18}{9}=2\)
Suy ra đpcm.
NP
8
TM
15 tháng 3 2015
- 3/10 +3/11 +3/12 +3/13 +3/14 > 3/15 + 3/15 +3/15 +3/15 +3/15 = 15/15 =1
S < 3/10 +3/10 +3/10 + 3/10 + 3/10 = 15/ 10 < 20/10 =2
LH
0
NP
1
TT
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2023
\(S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}\)
\(\Rightarrow S< \dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}\)
\(\Rightarrow S< \dfrac{15}{10}< 2\)
Lại có \(S>\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}\)
\(\Rightarrow S>\dfrac{15}{14}>1\)
\(\Rightarrow1< S< 2\)
TT
1
5 tháng 4 2016
Ta có: S =3/10+3/11+3/12+3/13+3/14 = 3.(1/10+1/11+1/12+1/13+1/14) > 3.(1/15 + 1/15 + 1/15 + 1/15 + 1/15) = 3.5/15 = 1 => S > 1 (1)
S=3/10+3/11+3/12+3/13+3/14 = 3.(1/10+1/11+1/12+1/13+1/14) < 3.(1/10 + 1/10 + 1/10 + 1/10 + 1/10) = 3.5/10 = 3/2<2 =>S <2 (2)
Từ (1) va (2)
=> 1 < S < 2 (đpcm).
Chúc bạn học tập tốt :)
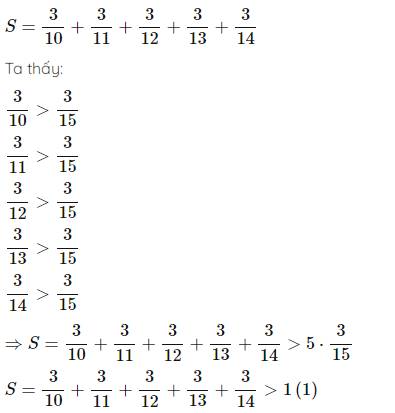
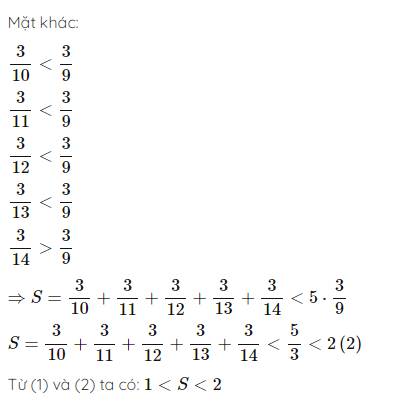
Mọi người tk mình đi!
Cảm ơn nhiều nha!!!!!!!!!!!!!!!!!!!!!!!!
???...!!!