Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì phương trình có 2 nghiệm phân biệt \(x_1,x_2\) nên theo hệ thức VI-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=m+5\\x_1x_2=3m+6\end{matrix}\right.\)
Mà \(x_1,x_2\) là độ dài của hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 5 nên ta có:\(\Rightarrow x_1^2+x_2^2=25\Rightarrow\left(x_1+x_2\right)^2-2x_1x_2=25\Rightarrow\left(m+5\right)^2-2\left(3m+6\right)=25\Leftrightarrow m^2+10m+25-6m-12=25\Leftrightarrow m^2+4m-12=0\Leftrightarrow m^2-2m+6m-12=0\Leftrightarrow\left(m-2\right)\left(m+6\right)=0\Leftrightarrow\left[{}\begin{matrix}m=2\\m=-6\end{matrix}\right.\) b Vì phương trình có 2 nghiệm phân biệt \(x_1,x_2\) nên theo hệ thức Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2m-6\\x_1x_2=2m-2\end{matrix}\right.\) \(\Rightarrow T=\left(x_1+x_2\right)^2-2x_1x_2=\left(2m-6\right)^2-2\left(2m-2\right)=4m^2-24m+36-4m+4=4m^2-28m+40=4m^2-28m+49-9=\left(2m-7\right)^2-9\ge-9\) Dấu = xảy ra \(\Leftrightarrow m=\dfrac{7}{2}\)

Đề là \(x^2-\left(m+5\right)x+3m+6=0\) đúng không nhỉ?
a. Ta có:
\(\Delta=\left(m+5\right)^2-4\left(3m+6\right)=m^2-2m+1=\left(m-1\right)^2\ge0\) ; \(\forall m\)
\(\Rightarrow\) Phương trình đã cho luôn có 2 nghiệm với mọi m
b. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+5\\x_1x_2=3m+6\end{matrix}\right.\)
Để \(x_1;x_2\) là độ dài 2 cạnh góc vuông thì trước hết \(x_1;x_2\) dương
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m+5>0\\3m+6>0\end{matrix}\right.\) \(\Rightarrow m>-2\)
Khi đó áp dụng định lý Pitago:
\(x_1^2+x_2^2=25\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=25\)
\(\Leftrightarrow\left(m+5\right)^2-2\left(3m+6\right)=25\)
\(\Leftrightarrow m^2+6m-12=0\Rightarrow\left[{}\begin{matrix}m=-3-\sqrt{21}< -2\left(loại\right)\\m=-3+\sqrt{21}\end{matrix}\right.\)

\(\Delta=\left(m+5\right)^2-4\left(3m+6\right)=m^2-2m+1=\left(m-1\right)^2\ge0\) ;\(\forall m\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+5\\x_1x_2=3m+6\end{matrix}\right.\)
Do \(x_1;x_2\) là độ dài 2 cạnh tam giác nên \(x_1>0;x_2>0\)
\(\Rightarrow\left\{{}\begin{matrix}m+5>0\\3m+6>0\end{matrix}\right.\) \(\Rightarrow m>-2\)
Khi đó, áp dụng định lý Pitago:
\(x_1^2+x_2^2=5^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=25\)
\(\Leftrightarrow\left(m+5\right)^2-2\left(3m+6\right)=25\)
\(\Leftrightarrow m^2+4m-12=0\Rightarrow\left[{}\begin{matrix}m=-6< -2\left(loại\right)\\m=2\end{matrix}\right.\)

a: Khi m=3 thì (1): x^2-3x+2*3-4=0
=>x^2-3x+2=0
=>x=1 hoặc x=2
b:
Δ=(-m)^2-4(2m-4)
=m^2-8m+16=(m-4)^2
Để phương trình có hai nghiệm phân biệt thì m-4<>0
=>m<>4
Theo đề, ta có: x1^2+x2^2=13
=>(x1+x2)^2-2x1x2=13
=>m^2-2(2m-4)=13
=>m^2-4m+8-13=0
=>m^2-4m-5=0
=>(m-5)(m+1)=0
=>m=5 hoặc m=-1

ta có
△=(m-2)2-4(m-3)=m2-4m+4-4m+12=m2-8m+16=(m-4)2
để phương trình có 2 nghiệm phân biệt thì △>0 suy ra m≠4
nhận xét:
x1,x2 là độ dài của 2 tam giác vuông cân mà x1,x2 phân biệt nên
x1=\(-x2\) vì độ dài thì sẽ bằng |x1| và |x2|
áp dụng hệ thức vi-et ta có:
\(\begin{cases} x1+x2=m-2(1)\\ x1x2=m-3(2) \end{cases}\)→x1+x2-1=x1x2 \(\Leftrightarrow \)(x1-1)(x2-1)=0
\(\Leftrightarrow \)\(\left[\begin{array}{} x1=1\\ x2=1 \end{array} \right.\)\(\Leftrightarrow \)x1x2=-1(vì x1=-x2) \(\Leftrightarrow \)m-3=-1\(\Leftrightarrow \)m=2
vậy m=2 thì....

a: Khi m=-3 thì (1): x^2-(-x)-2=0
=>x^2+x-2=0
=>x=-2 hoặc x=1
b: Δ=(m+2)^2-4(m+1)
=m^2+4m+4-4m-4=m^2>=0
=>Phương trình luôn có 2 nghiệm


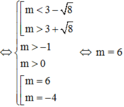
Để phương trình có 2 nghiệm:
\(\Delta\ge0\Rightarrow\left[-\left(m+2\right)\right]^2-4.1.\left(3m-3\right)\ge0\\ \Leftrightarrow m^2+4m+4-12m+12\ge0\\ \Leftrightarrow m^2-8m+16\ge0\forall m\)
Theo Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left[-\left(m+2\right)\right]}{1}=m+2\\x_1.x_2=\dfrac{3m-3}{1}=3m-3\end{matrix}\right.\)
x1, x2 là độ dài của một giam giác vuông có cạnh huyền bằng 5.
Theo định lý Py-ta-go ta có:
\(x_1^2+x_2^2=5^2\Leftrightarrow x_1^2+2x_1x_2+x_2^2-2x_1x_2=25\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=25\\ \Leftrightarrow\left(m+2\right)^2-2.\left(3m-3\right)=25\\ \Leftrightarrow m^2+4m+4-6m+6-25=0\\ \Leftrightarrow m^2-2m-15=0\Leftrightarrow\left[{}\begin{matrix}m=5\\m=-3\end{matrix}\right.\)
Vậy...