Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta thấy pt luôn có no . Theo hệ thức Vi - ét ta có:
x1 + x2 = \(\dfrac{-b}{a}\) = 6
x1x2 = \(\dfrac{c}{a}\) = 1
a) Đặt A = x1\(\sqrt{x_1}\) + x2\(\sqrt{x_2}\) = \(\sqrt{x_1x_2}\)( \(\sqrt{x_1}\) + \(\sqrt{x_2}\) )
=> A2 = x1x2(x1 + 2\(\sqrt{x_1x_2}\) + x2)
=> A2 = 1(6 + 2) = 8
=> A = 2\(\sqrt{3}\)
b) bạn sai đề

a) 2x2 – 17x + 1 = 0 có a = 2, b = -17, c = 1
∆ = (-17)2 – 4 . 2 . 1 = 289 – 8 = 281
x1 + x2 = =
; x1x2 =
b) 5x2 – x + 35 = 0 có a = 5, b = -1, c = -35
∆ = (-1)2 – 4 . 5 . (-35) = 1 + 700 = 701
x1 + x2 = =
; x1x2 =
= -7
c) 8x2 – x + 1 = 0 có a = 8, b = -1, c = 1
∆ = (-1)2 – 4 . 8 . 1 = 1 - 32 = -31 < 0
Phương trình vô nghiệm nên không thể điền vào ô trống được.
d) 25x2 + 10x + 1 = 0 có a = 25, b = 10, c = 1
∆ = 102 – 4 . 25 . 1 = 100 - 100 = 0
x1 + x2 = =
; x1x2 =
a) 2x2 – 17x + 1 = 0 có a = 2, b = -17, c = 1
∆ = (-17)2 – 4 . 2 . 1 = 289 – 8 = 281
x1 + x2 = =
; x1x2 =
b) 5x2 – x + 35 = 0 có a = 5, b = -1, c = -35
∆ = (-1)2 – 4 . 5 . (-35) = 1 + 700 = 701
x1 + x2 = =
; x1x2 =
= -7
c) 8x2 – x + 1 = 0 có a = 8, b = -1, c = 1
∆ = (-1)2 – 4 . 8 . 1 = 1 - 32 = -31 < 0
Phương trình vô nghiệm nên không thể điền vào ô trống được.
d) 25x2 + 10x + 1 = 0 có a = 25, b = 10, c = 1
∆ = 102 – 4 . 25 . 1 = 100 - 100 = 0
x1 + x2 = =
; x1x2 =

Câu c làm tương tự, mẫu số nhân ra và nhóm lại theo dạng: x1+x2 và x1.x2
TOÁN HỌC
Toán lớp 2
Bài 1, bài 2, bài 3, bài 4, bài 5 tiết 92.luyện tập (trang 96 sgk)
Bài 1: Số ?,Bài 2: Tính (theo mẫu),Bài 3: Mỗi xe đạp có hai bánh xe. Hỏi 8 xe đạp có bao nhiêu bánh xe ? Bài 4: Viết số thích hợp vào ô trống (theo mẫu),Bài 5: Viết số thích hợp vào ô trống (theo mẫu):
- Lý thuyết, bài 1, bài 2, bài 3 tiết 93.bảng nhân 3 (trang 97sgk)
- Bài 1, bài 2, bài 3, bài 4, bài 5 tiết 94.luyện tập (trang 98 sgk)
- Lý thuyết, bài 1, bài 2, bài 3 tiết 95. bảng nhân 4 (trang 99 sgk)
- Bài 1, bài 2, bài 3, bài 4 tiết 96.luyện tập (trang 100 sgk)
Xem thêm: CHƯƠNG V: PHÉP NHÂN VÀ PHÉP CHIA
Bài 1: Số ?
Bài 2: Tính (theo mẫu)
2cm x 3 = 6cm 2kg x 4 =
2cm x 5 = 2kg x 6 =
2dm x 8 = 2kg x 9 =
Bài 3: Mỗi xe đạp có hai bánh xe. Hỏi 8 xe đạp có bao nhiêu bánh xe ?
Bài 4: Viết số thích hợp vào ô trống (theo mẫu):
Bài 5: Viết số thích hợp vào ô trống (theo mẫu):
Bài giải:
Bài 1:
Bài 2:
2cm x 3 = 6cm 2kg x 4 = 8kg
2cm x 5 = 10cm 2kg x 6 = 12kg
2dm x 8 = 16cm 2kg x 9 = 18kg
Bài 3:
Số bánh xe của 78 xe đạp là:
2 x 8 = 16 (bánh xe)
Đáp số: 16 bánh xe.
Bài 4: Hướng dẫn: Điền lần lượt từ trái sang phải vào các ô trống còn lại là: 12, 18, 20, 14, 10, 16, 4.
Bài 5:
Hướng dẫn: Điền lần lượt từ trái sang phải vào các ô trống các số là: 10, 14, 18, 20, 4.
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 1, bài 2, bài 3, bài 4, bài 5 trang 180 sgk toán lớp 2 (12/01)
- Bài 1, bài 2, bài 3, bài 4, bài 5 trang 180,181 sgk toán lớp 2 (12/01)
- Bài 1, bài 2, bài 3, bài 4, bài 4 trang 177, 178 sgk toán lớp 2 (12/01)
- Bài 1, bài 2, bài 3, bài 4 trang 178,179 sgk toán lớp 2 (12/01)
- Bài 1, bài 2, bài 3, bài 4, bài 5 trang 181 sgk toán lớp 2 (12/01)
Xem thêm tại: http://loigiaihay.com/bai-1-bai-2-bai-3-bai-4-bai-5-tiet-92luyen-tap-c114a15865.html#ixzz4bgVSXCQi

x1;x2 là nghiệm của pt
=> \(x^2_1-3\sqrt{2}x_1-\sqrt{2}=0\Rightarrow x^2_1=3\sqrt{2}x_1+\sqrt{2}\)
\(x^2_2-3\sqrt{2}x_2-\sqrt{2}=0\Rightarrow x^2_2=3\sqrt{2}x_2+\sqrt{2}\)
=> \(A=\frac{2}{3\sqrt{2}x_1+3\sqrt{2}x_2+\sqrt{2}-3\sqrt{2}}+\frac{3\sqrt{2}x_2+3\sqrt{2}x_1+\sqrt{2}-3\sqrt{2}}{2}\)
\(A=\frac{2}{3\sqrt{2}\left(x_1+x_2\right)-2\sqrt{2}}+\frac{3\sqrt{2}\left(x_2+x_1\right)-2\sqrt{2}}{2}\)
Theo VI ét => \(x_1+x_2=3\sqrt{2}\). Thay vào A
=> quy đồng.....

đúng r đó bn, nhìn nè:
\(\left(x_1-x_2\right)\left(x_1x_2+1\right)=x_1^2x_2+x_1-x_1x_2^2-x_2\)
Để pt (1) có nghiệm thì: \(\Delta>0\)\(\Leftrightarrow m^2+4>0\)
\(\Rightarrow\)đúng với \(\forall m\) ( vì \(m^2>0\) và 4 hiển nhiên >0)
theo viet, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-1\end{matrix}\right.\)
ta có \(P=\dfrac{x_1^2+x_1-1}{x_1}-\dfrac{x_2^2+x_2-1}{x_2}\)
\(\Leftrightarrow P=\dfrac{x_1^2x_2+x_1x_2-x_2-x_1x_2^2-x_1x_2+x_1}{x_1x_2}\)
\(\Leftrightarrow P=\dfrac{\left(x_1-x_2\right)\left(x_1x_2+1\right)}{x_1x_2}=\dfrac{\left(x_1-x_2\right)0}{x_1x_2}\)( vì \(x_1x_2=-1\) mà -1+1=0)
\(\Leftrightarrow P=0\)

pt có 2 nghiệm pb dương
<=> {delta=25-4m>0
{ x1+x2=5>0
{x1..x2=m>0
<=> 0<m <25/4
( x1canx2+x2canx1)2=36
x1^2..x2 +x1 ..x2^2 +2 (x1×x2)can (x1×x2)=36
sau đó sử ddụng viet và thay vào
mn cho mk hỏi
nếu đđặt câu hỏi trên OLM này thì khi có người giải đáp cho mk thì có thông báo k z
Lập \(\Delta=25-4m\)
Phương trình có 2 nghiệm \(x_1;x_2\)khi \(\Delta\ge0\)hay \(m\le\frac{25}{4}\)
Áp dụng hệ thức Vi-et ta có \(\hept{\begin{cases}x_1+x_2=5\\x_1x_2=m\end{cases}}\)
2 nghiệm \(x_1;x_2\)dương khi \(\hept{\begin{cases}x_1+x_2>0\\x_1x_2>0\end{cases}}\)hay m>0
Điều kiện để pt có 2 nghiệm dương x1;x2 là \(0< m< \frac{25}{4}\)(*)
Ta có \(\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=x_1+x_2+2\sqrt{x_1x_2}=5+2\sqrt{m}\)
=> \(\sqrt{x_1}+\sqrt{x_2}=\sqrt{5+2\sqrt{m}}\)
Ta có \(x_1\sqrt{x_2}+x_2\sqrt{x_1}=6\Leftrightarrow\sqrt{x_1x_2}\left(\sqrt{x_1}+\sqrt{x_2}\right)=6\)
hay \(\sqrt{m}\sqrt{5+2\sqrt{m}}=6\Leftrightarrow2m\sqrt{m}+5m-36=0\left(1\right)\)
Đặt \(t=\sqrt{m}\ge0\)khi đó (1) trở thành
\(\Leftrightarrow2t^2+5t^2-36=0\)
\(\Leftrightarrow\left(t-2\right)\left(2t^2+9t+18\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t-2=0\\2t^2+9t+18=0\end{cases}\Rightarrow t=2\Rightarrow m=4\left(tmđk\right)}\)
(vì 2t2+9t+18 vô nghiệm)
Vậy m=4 thì pt đã cho có 2 nghiệm dương x1;x2 thỏa mãn \(x_1\sqrt{x_2}+x_2\sqrt{x_1}=6\)

a) Tam thức bậc hai có \(\Delta'=m^2-m+4=m^2-2.\frac{1}{2}m+\frac{1}{4}-\frac{1}{4}+4=\left(m-\frac{1}{2}\right)^2+\frac{15}{4}>0\).
Suy ra phương trình (1) luôn có nghiệm với mọi m.
b) Theo Vi-et ta có:
\(x_1+x_2=2m,x_1.x_2=m-4\)
Điều kiển để \(x_1+x_2=\frac{x_1^2}{x_2}+\frac{x_2^2}{x_1}\)
\(\Leftrightarrow x_1+x_2=\frac{x_1^3+x_2^3}{x_1x_2}\)
\(\Leftrightarrow x_1+x_2=\frac{\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)}{x_1x_2}\)
\(\Leftrightarrow2m=\frac{\left(2m\right)^3-3\left(m-4\right).2m}{m-4}\)
\(\Leftrightarrow2m\left(m-4\right)=8m^3-6m^2+8m\) và \(m\ne4\)
\(\Leftrightarrow4m\left(2m^2-2m+3\right)=0\) và \(m\ne4\)
\(\Leftrightarrow m=0\)
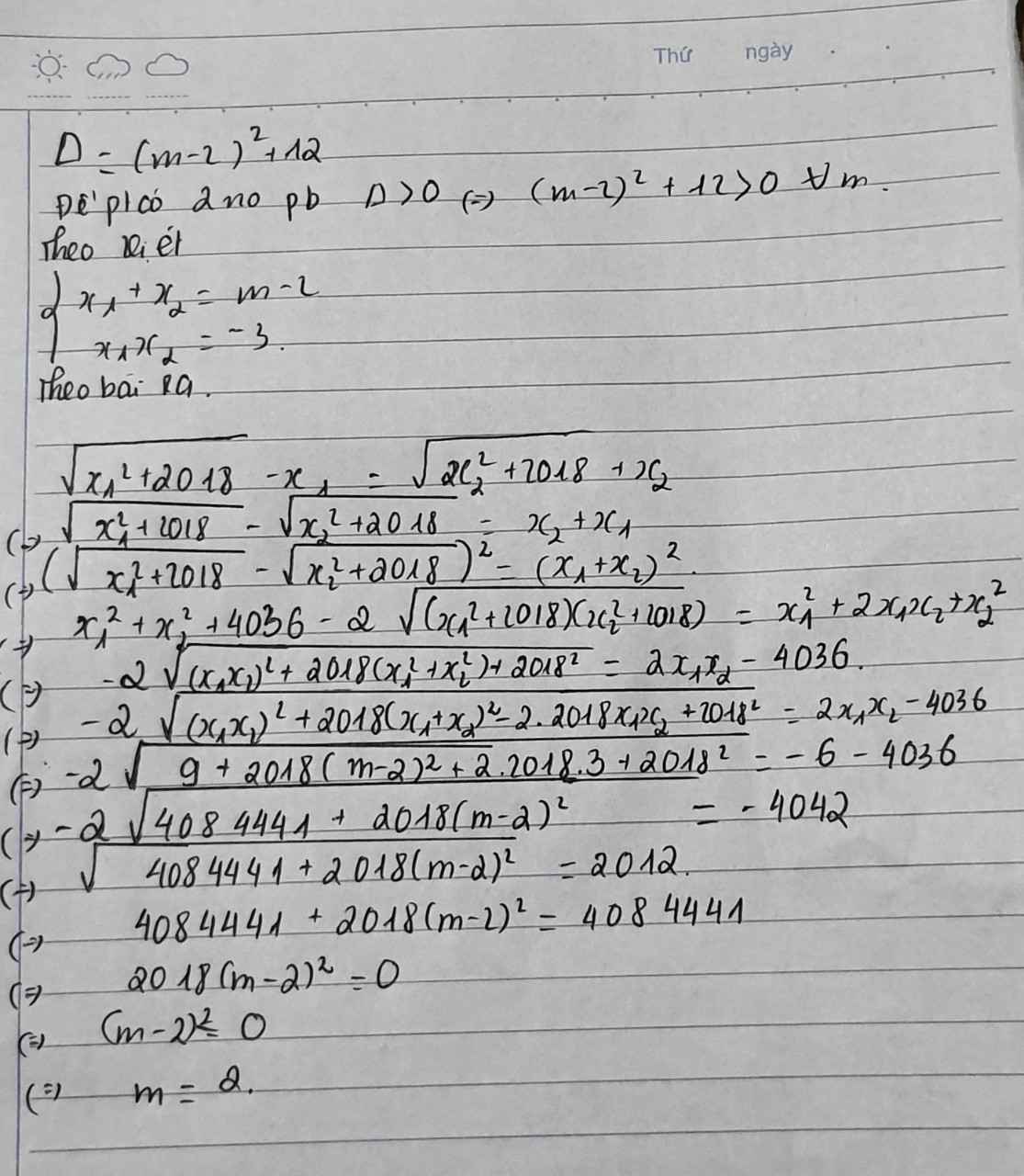
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=6\\x_1x_2=8\end{matrix}\right.\)
Theo đề:
\(B=\dfrac{x_1\sqrt{x_1}-x_2\sqrt{x_2}}{x_1-x_2}=\dfrac{\left(\sqrt{x_1}-\sqrt{x_2}\right)\left(x_1+\sqrt{x_1x_2}+x_2\right)}{\left(\sqrt{x_1}-\sqrt{x_2}\right)\left(\sqrt{x_1}+\sqrt{x_2}\right)}\left(x_1,x_2\ge0\right)\)
\(=\dfrac{6+\sqrt{8}}{\sqrt{x_1}+\sqrt{x_2}}\)
Tính: \(\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=x_1+x_2+2\sqrt{x_1x_2}=6+2\sqrt{8}=6+4\sqrt{2}=\left(\sqrt{4}+\sqrt{2}\right)^2\)
\(\Rightarrow\sqrt{x_1}+\sqrt{x_2}=\sqrt{4}+\sqrt{2}\) (thỏa mãn \(x_1,x_2\ge0\))
Khi đó: \(P=\dfrac{6+\sqrt{8}}{\sqrt{4}+\sqrt{2}}=4-\sqrt{2}\)
bạn gthich giúp mình trên tử với ạ