Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Đặt x 2 = t (t ≥ 0). Khi đó ta có phương trình: t 2 – mt – m – 1 = 0 (*)
Δ = m 2 - 4(-m - 1) = m 2 + 4m + 4 = m + 2 2
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
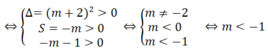

a)Thay m=-7 vào pt ta được: \(x^4+5x^2-14=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=2\\x^2=-7\left(L\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
Vậy...
b) Đặt \(t=x^2\left(t\ge0\right)\)
=>Với mỗi t dương ta tìm được hai nghiệm x phân biệt
Pttt: \(t^2-\left(m+2\right)t+3m+7=0\) (*)
Để pt ban đầu có hai nghiệm pb <=> pt (*) có 1 nghiệm dương duy nhất hoặc có hai nghiệm phân biệt trái dấu
TH1:PT (*) có 1 nghiệm dương duy nhất
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=0\\-\dfrac{b}{2a}>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2-8m-24=0\\\dfrac{m+2}{2}>0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=4+2\sqrt{10}\\m=4-2\sqrt{10}\end{matrix}\right.\\m>-2\end{matrix}\right.\)\(\Rightarrow m=4+2\sqrt{10}\) (1)
TH2: Pt (*) có hai nghiệm phân biệt trái dấu
\(\Leftrightarrow ac< 0\) \(\Leftrightarrow3m+7< 0\) \(\Leftrightarrow m< -\dfrac{7}{3}\) (2)
Từ (1) (2) =>\(\left[{}\begin{matrix}m=4+2\sqrt{10}\\m< -\dfrac{7}{3}\end{matrix}\right.\)
trông kết quả em tự làm ra không được tròn nên em gửi câu hỏi lên đây. Hóa ra mình làm đúng (??????)

Theo viet ta có
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-2m\end{matrix}\right.\)
Ta có: \(x_1^2+x_1-x_2=5-2m\)
\(\Leftrightarrow x_1^2+x_1-x_2=5+x_1x_2\)
\(\Leftrightarrow\left(x_1^2+x_1\right)-\left(x_2-x_1x_2\right)=5\)
\(\Leftrightarrow x_1\left(x_1+1\right)-x_2\left(x_1+1\right)=5\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1+1\right)=5\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x_1-x_2=1\\x_1+1=5\end{matrix}\right.\\\left\{{}\begin{matrix}x_1-x_2=5\\x_1+1=1\end{matrix}\right.\end{matrix}\right.\)
-Với \(\left\{{}\begin{matrix}x_1-x_2=1\\x_1+1=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_2=3\\x_1=4\end{matrix}\right.\)
\(\Rightarrow x_1x_2=12=-2m\)
\(\Rightarrow m=-6\)
-Với \(\left\{{}\begin{matrix}x_1-x_2=5\\x_1+1=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_2=-5\\x_1=0\end{matrix}\right.\)
\(\Rightarrow x_1.x_2=0=-2m\)
\(\Rightarrow m=0\)
Vậy \(m=0;m=-6\)
-Chúc bạn học tốt-

a)PT có 2 nghiệm phân biệt
`<=>Delta>0`
`<=>(2m+3)^2+4(2m+4)>0`
`<=>4m^2+12m+9+8m+16>0`
`<=>4m^2+20m+25>0`
`<=>(2m+5)^2>0`
`<=>m ne -5/2`
b)Áp dụng vi-ét:
$\begin{cases}x_1+x_2=2m+3\\x_1.x_2=-2m-4\\\end{cases}$
`|x_1|+|x_2|=5`
`<=>x_1^2+x_2^2+2|x_1.x_2|=25`
`<=>(x_1+x_2)^2+2(|x_1.x_2|-x_1.x_2)=25`
`<=>(2m+3)^2+2[|-2m-4|-(-2m-4)]=25`
Với `-2m-4>=0<=>m<=-2`
`=>pt<=>(2m+3)^2-25=0`
`<=>(2m-2)(2m+8)=0`
`<=>(m-1)(m+4)=0`
`<=>` $\left[ \begin{array}{l}x=1\\x=-4\end{array} \right.$
`-2m-4<=0=>m>=-2=>|-2m-4|=2m+4`
`<=>4m^2+12m+9+8m+16=25`
`<=>4m^2+20m=0`
`<=>m^2+5m=0`
`<=>` \left[ \begin{array}{l}x=0\\x=-5\end{array} \right.$
Vậy `m in {0,1,-4,-5}`

Δ=(m+2)^2-4*2m=(m-2)^2
Để PT có hai nghiệm pb thì m-2<>0
=>m<>2
\(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1x_2}{4}\)
=>\(\dfrac{x_1+x_2}{x_1x_2}=\dfrac{x_1x_2}{4}\)
=>\(\dfrac{m+2}{2m}=\dfrac{2m}{4}=\dfrac{m}{2}\)
=>2m^2=2m+4
=>m^2-m-2=0
=>m=2(loại) hoặc m=-1
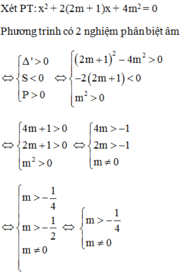
Đặt \(x^2=t\left(t\ge0\right)\), phương trình trở thành:
\(t^2-2\left(m+1\right)t+2m+1=0\left(1\right)\)
Yêu cầu bài toán thỏa mãn khi phương trình \(\left(1\right)\) có hai nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2>0\\t_1+t_2=2m+2>0\\t_1t_2=2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{2}\\m\ne0\end{matrix}\right.\)