Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hằng đẳng thức:
\(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
Ta thấy \(\left(x-1\right)+\left(x-2\right)+\left(3-2x\right)=0\)
do đó \(\left(x-1\right)^3+\left(x-2\right)^3+\left(3-2x\right)^3=3\left(x-1\right)\left(x-2\right)\left(3-2x\right)\)
suy ra \(\left(x-1\right)\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x_1=1\\x_2=2\\x_3=\frac{3}{2}\end{cases}}\)
\(S=\frac{29}{4}\).

Với m = 1 ta có phương trình:
\(x^2-2x+1=0\)
Sử dụng đen ta ta có: \(\Delta=\left(-2\right)^2-4.1.1=0\)
nên phương trình có nghiệm kép \(x_1=x_2=\frac{2}{2}=1\)
Vậy phương trình trên có nghiệm x = 1
b) Đặt phương trình \(x^2-\left(3m-1\right)x+2m^2-m=0\left(1\right)\) \(\Rightarrow\Delta>0\)
\(\Leftrightarrow\left[-\left(3m-1\right)\right]^2-4.1.\left(2m^2-m\right)>0\)
\(\Leftrightarrow\left(3m-1\right)^2-4\left(2m^2-m\right)>0\)
\(\Leftrightarrow9m^2-6m+1-8m^2+4m>0\)
\(\Leftrightarrow m^2-2m+1>0\)
\(\Leftrightarrow\left(m-1\right)^2>0\Leftrightarrow m-1\ne0\Leftrightarrow m\ne1\)
\(\left|x_1-x_2\right|-2=0\Leftrightarrow\left|x_1-x_2\right|=2\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=4\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4\)\(\left(2\right)\)
Áp dụng hệ thức Vi-ét cho phương trình ( 1 ) ta có:
\(\hept{\begin{cases}x_1+x_2=3m-1\\x_1x_2=2m^2-m\end{cases}}\)
từ ( 2 ) suy ra \(\left(3m-1\right)^2-4\left(2m^2-m\right)=4\)
\(\Leftrightarrow9m^2-6m+1-8m^2+4m=4\)
\(\Leftrightarrow m^2-2m+1-4=0\)
\(\Leftrightarrow m^2-2m-3=0\Leftrightarrow\)\(\left(m+1\right)\left(m-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}m+1=0\\m-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}m=-1\left(tmđk\right)\\m=3\left(tmđk\right)\end{cases}}}\)
Vậy \(m=-1;m=3\)thỏa mãn yêu cầu đề bài đã cho

\(\frac{x+4}{2000}+\frac{x+3}{2001}=\frac{x+2}{2002}+\frac{x+1}{2003}\)
\(\Leftrightarrow2+\frac{x+4}{2000}+\frac{x+3}{2001}=2+\frac{x+2}{2002}+\frac{x+1}{2003}\)
\(\Leftrightarrow\left(\frac{x+4}{2000}+1\right)+\left(\frac{x+3}{2001}+1\right)=\left(\frac{x+2}{2002}+1\right)+\left(\frac{x+1}{2001}+1\right)\)
\(\Leftrightarrow\frac{x+2004}{2000}+\frac{x+2004}{2001}=\frac{x+2004}{2002}+\frac{x+2004}{2003}\)
\(\Leftrightarrow\left(x+2004\right)\left(\frac{1}{2000}+\frac{1}{2001}-\frac{1}{2002}-\frac{1}{2003}\right)=0\)
Mà \(\frac{1}{2000}+\frac{1}{2001}-\frac{1}{2002}-\frac{1}{2003}\ne0\)
Suy ra x+2004=0
\(\Leftrightarrow x=-2004\)
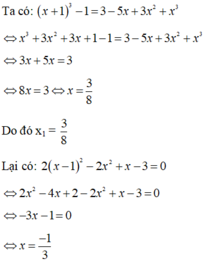
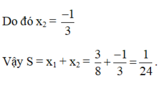
Để phương trình có 2 nghiệm \(x_1;x_2\)thì \(\Delta=\left(m+2\right)^2-4\left(2m-1\right)=m^2=4m+4-8m+4=m^2-4m+8\)
\(=\left(m-2\right)^2+4>0\forall m\)
Nên phương trình luôn có 2 nghiệm phân biệt với mọi m
Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=m+2\\x_1.x_2=2m-1\end{cases}\Rightarrow\hept{\begin{cases}2x_1+2x_2=2m+4\\x_1.x_2=2m-1\end{cases}}}\Rightarrow2x_1+2x_2-x_1.x_2=5\)
Vậy hệ thức giữa \(x_1;x_2\)độc lập với m là \(2x_1+2x_2-x_1.x_2=5\)