Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Khi m=-2 thì phương trình sẽ là \(x^2-8x-9=0\)
=>(x-9)(x+1)=0
=>x=9 hoặc x=-1
b: \(\text{Δ}=\left(4m\right)^2-4\left(4m-1\right)\)
\(=16m^2-16m+4=\left(4m-2\right)^2>=0\)
Để phương trình có hai nghiệm phân biệt thì 4m-2<>0
hay m<>1/2
`a)` Thay `m=-2` vào ptr có:
`x^2+4.(-2)x+4.(-2)-1=0`
`<=>x^2-8x-9=0`
Ptr có: `a-b+c=1-(-8)+(-9)=0`
`=>x_1=-1;x_2=[-c]/a=9`
Vậy với `m=-2` thì `S={-1;9}`
_____________________________________________
`b)` Ptr có `2` nghiệm pb
`<=>\Delta' > 0`
`<=>(2m)^2-(4m-1) > 0`
`<=>4m^2-4m+1 > 0`
`<=>(2m-1)^2 > 0`
`=>(2m-1)^2 \ne 0`
`<=>2m-1 \ne 0<=>m \ne 1/2`
Vậy ...........
a) Pt có hai nghiệm trái dấu \(\Leftrightarrow ac< 0\Leftrightarrow m< 0\)
b) Pt có nghiệm khi \(\Delta\ge0\Leftrightarrow36-4m\ge0\Leftrightarrow m\le9\)
Áp dụng hệ thức viet có:
\(\left\{{}\begin{matrix}x_1+x_2=6\left(1\right)\\x_1x_2=m\left(2\right)\end{matrix}\right.\)
Từ (1) kết hợp với điều kiện có:\(\left\{{}\begin{matrix}x_1+x_2=6\\x_1-2x_2=m\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}3x_2=6-m\\x_1+x_2=6\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{6-m}{3}\\x_1=6-x_2=\dfrac{12+m}{3}\end{matrix}\right.\)
\(\Rightarrow x_1x_2=\dfrac{6-m}{3}.\dfrac{12+m}{3}=m\)
\(\Leftrightarrow72-15m-m^2=0\)
\(\Delta=3\sqrt{57}\)
\(\Rightarrow m=\dfrac{-15\pm3\sqrt{57}}{2}\) (thỏa mãn)
Vậy...
a) Thay x=0 vào phương trình, ta được:
\(4\cdot0^2-2\cdot\left(2m+3\right)\cdot0+m+1=0\)
\(\Leftrightarrow m+1=0\)
hay m=-1
Áp dụng hệ thức Vi-et, ta có:
\(x_1+x_2=\dfrac{2\left(2m+3\right)}{4}\)
\(\Leftrightarrow x_1=\dfrac{2\cdot\left(-2+3\right)}{4}=\dfrac{2}{4}=\dfrac{1}{2}\)
Vậy: Khi m=-1 và nghiệm còn lại là \(x=\dfrac{1}{2}\)
a) Đây là phương trình bậc 2 ẩn x có
Δ = (-m)2 - 4(m-1)
= m2-4m+4 = (m-2)2
Do (m-2)2≥0 ∀m => Δ≥0 ∀m
Vậy phương trình luôn có nghiệm với mọi m.
b) Theo Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=m\left(1\right)\\x_1x_2=m-1\left(2\right)\end{matrix}\right.\)
\(x_1=2x_2\left(3\right)\)
Từ (1)(3) ta có hệ phương trình: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1=2x_2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}3x_2=m\\x_1=2x_2\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x_2=\dfrac{m}{3}\\x_1=\dfrac{2m}{3}\end{matrix}\right.\)
Thay \(x_1=\dfrac{2m}{3};x_2=\dfrac{m}{3}\) vào (2) ta có:
\(\dfrac{2m}{3}.\dfrac{m}{3}=m-1\)
<=> 2m2 = 9(m - 1)
<=> 2m2 - 9m + 9 = 0
<=> (m - 3)(2m - 3) = 0
<=> \(\left[{}\begin{matrix}m-3=0\\2m-3=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}m=3\\m=\dfrac{3}{2}\end{matrix}\right.\)
Vậy tại m ∈\(\left\{3;\dfrac{3}{2}\right\}\) thì hai nghiệm của phương trình thoả mãn x1=2x2
a) Ta có:
\(\Delta=b^2-4ac=\left(-m\right)^2-4.1.\left(m-1\right)\)
\(=m^2-4m+4=\left(m-2\right)^2\ge0\) với mọi m
Vậy phương trình đã cho luôn có nghiệm với mọi m
b) Do phương trình luôn có nghiệm với mọi m
Theo định lý Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left(-m\right)}{1}=m\left(1\right)\\x_1x_2=\dfrac{c}{a}=\dfrac{m-1}{1}=m-1\left(2\right)\end{matrix}\right.\)
Mà \(x_1=2x_2\), thay vào (1) ta có:
\(2x_2+x_2=3\Leftrightarrow3x_2=m\Leftrightarrow x_2=\dfrac{m}{3}\)
\(\Rightarrow x_1=2x_2=\dfrac{2m}{3}\)
Thay \(x_1=\dfrac{2m}{3};x_2=\dfrac{m}{3}\) vào (2) ta có:
\(\dfrac{2m}{3}.\dfrac{m}{3}=m-1\)
\(\Leftrightarrow2m^2=9m-9\)
\(\Leftrightarrow2m^2-9m+9=0\) (*)
\(\Delta_m=\left(-9\right)^2-4.2.9=9\)
Phương trình (*) có 2 nghiệm:
\(m_1=\dfrac{-\left(-9\right)+\sqrt{9}}{2.2}=3\)
\(m_2=\dfrac{-\left(-9\right)-\sqrt{9}}{2.2}=\dfrac{3}{2}\)
Vậy \(m=3;m=\dfrac{3}{2}\) thì phương trình đã cho có hai nghiệm \(x_1;x_2\) thỏa mãn \(x_1=2x_2\)
a,\(\Delta'=\left(-m\right)^2-1.1=m^2-1\)
b,Để pt có nghiệm kép thì \(\Delta'=0\)
\(\Leftrightarrow m^2-1=0\Leftrightarrow m^2=1\Leftrightarrow m=\pm1\)
Vậy......
Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m >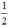 
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m =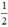 
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m <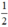 
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m <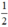 
; có nghiệm kép khi m = 
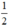và vô nghiệm khi m >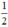 
a/ Xét pt :
\(x^2-2\left(m-1\right)+2m-5=0\)
\(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-2m+1-2m+5=m^2-4m+6=\left(m-2\right)^2+2>0\forall m\)
\(\Leftrightarrow\) pt luôn có 2 nghiệm pb với mọi m
b/ Phương trình cớ 2 nghiệm trái dấu
\(\Leftrightarrow2m-5< 0\)
\(\Leftrightarrow m< \dfrac{5}{2}\)
c/ Theo định lí Vi - et ta có :
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1.x_2=2m-5\end{matrix}\right.\)
\(A=x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^2-2x_1.x_2\)
\(=4\left(m-1\right)^2-2\left(2m-5\right)\)
\(=4m^2-8m+4-4m+10\)
\(=4m^2-12m+14=4\left(m^2-3m+\dfrac{9}{4}\right)+5=4\left(m-\dfrac{3}{2}\right)^2+5\ge5\)
\(A_{min}=5\Leftrightarrow m=\dfrac{3}{2}\)
1, \(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-4m+6=\left(m-2\right)^2+2>0\)
Vậy pt luôn có 2 nghiệm pb với mọi m
2, Vì pt có 2 nghiệm trái dấu
\(x_1x_2=\dfrac{c}{a}=2m-5< 0\Leftrightarrow m< \dfrac{5}{2}\)
3, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=2m-5\end{matrix}\right.\)
\(A=\left(x_1+x_2\right)^2-2x_1x_2=4\left(m-1\right)^2-2\left(2m-5\right)\)
\(=4m^2-12m+14=4m^2-2.2m.3+9+6\)
\(=\left(2m-3\right)^2+6\ge6\forall m\)
Dấu ''='' xảy ra khi m = 3/2
Vậy với m = 3/2 thì A đạt GTNN tại 6
\(x^{2^{ }}+2\left(m-1\right)x-6m-7=0\left(1\right)\)
a) \(Dental=\left[2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-6m-7\right)\)
\(< =>4\cdot\left(m^2-2m+1\right)+24m+28\)
\(< =>4m^2-8m+4+24m+28\)
\(< =>4m^2+16m+32\)
\(< =>\left(2m+4\right)^2+16>0\) với mọi m
Vậy phương (1) luôn có 2 nghiệm phân biệt với mọi m
b) Theo định lí vi ét ta có:
x1+x2= \(\dfrac{-2\left(m-1\right)}{1}=-2m+1\)
x1x2= \(-6m-7\)
quy đồng
khử mẫu
tách sao cho có tích và tổng
thay x1x2 x1+x2
kết luận
mặt xấu vl . . .
b > Để pt 1 có 2 nghiệm phân biệt
=> \(\Delta>0\) <=> \(3^2-4\left(m-3\right)>0\)
<=> 9 -4m +12 >0
<=> -4m+21>0
<=> m<\(\dfrac{21}{4}\)
Vậy m<\(\dfrac{21}{4}\) là giá trị cần tìm tm yc đề bài
phần a tự giải nha bạn