Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Δ=(-4)^2-4(2m-2)
=16-8m+8=-8m+24
Để phương trình có hai nghiệm phân biệt thì -8m+24>0
=>m<3
x1+x2=2x1x2
=>2(2m-2)=4
=>2m-2=2
=>2m=4
=>m=2(nhận)

a)thay m=1 vào pt ta có
\(x^2+4x=0\)
<=> \(\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
b) thay x=2 vào pt ta có: 13+m=0
<=>m=-13
thay m=-13 vào pt ta có
\(x^2+4x-12=0\)
<=>(x-2)(x+6)=0
<=>\(\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)\(\)
vậy với m=-13 thì nghiệm còn lại là x=-6
c) để pt có 2 nghiệm pb thì \(\Delta>0\)
<=>16-4m-4>0
<=>3-m>0
<=>m<3
áp dụng định lí Vi-ét ta có\(\left\{{}\begin{matrix}x_1+x_2=-4\\x_1x_2=m+1\end{matrix}\right.\)
theo đề bài ta có \(x_1^2+x_2^2=10\)
<=>\(\left(x_1+x_2\right)^2-2x_1x_2=10\)
<=>16-2m-2=10
<=>2-m=0
<=>m=2(nhận)
vậy với m=2 thì pt có 2 nghiệm pb thỏa yêu cầu đề bài.

a) Khi m = -5 ta được phương trình x2 + 4x - 5 = 0
Ta có a + b + c = 1 + 4 + (-5) = 0 nên phương trình có hai nghiệm phân biệt là x1 = 1; x2= c/a = (-5)/1 = -5
Tập nghiệm của phương trình S = {1; -5}
b) Δ' = 22 - m = 4 - m
Phương trình có nghiệm kép ⇔ Δ'= 0 ⇔ 4 - m = 0 ⇔ m = 4
c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4
Theo Vi-et ta có:
Ta có: x12 + x22 = 10 ⇔ (x1 + x2)2 - 2x1x2 = 10
⇔ (-4)2 - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)

`a)` Ptr có:`\Delta' =[-(m-1)]^2-(-3-m)`
`=m^2-2m+1+3+2m=m^2+4 > 0 AA m`
`=>` Ptr có `2` nghiệm `AA m`
`b) AA m`, áp dụng Vi-ét có:`{(x_1+x_2=[-b]/a=2m-2),(x_1.x_2=c/a=-3-m):}`
Ta có:`x_1 ^2+x_2 ^2 >= 10`
`<=>(x_1+x_2)^2-2x_1.x_2 >= 10`
`<=>(2m-2)^2-2(-3-m) >= 10`
`<=>4m^2-8m+4+6+2m >= 10`
`<=>4m^2-6m+10 >= 10`
`<=>4m^2-6m >= 0`
`<=>2m(2m-3) >= 0`
`<=>` $\left[\begin{matrix} m \ge \dfrac{3}{2}\\ m \le 0\end{matrix}\right.$
Vậy `m >= 3/2` hoặc `m <= 0` thì t/m yêu cầu đề bài
a: \(\text{Δ}=\left(2m-2\right)^2-4\left(-m-3\right)\)
\(=4m^2-8m+4+4m+12=4m^2-4m+16\)
\(=\left(2m-1\right)^2+15>0\)
Do đó: Phương trình luôn có hai nghiệm
b: Theo Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=-m-3\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2>=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2>=10\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(-m-3\right)>=10\)
\(\Leftrightarrow4m^2-8m+4+2m+6-10>=0\)
\(\Leftrightarrow4m^2-6m>=0\)
=>2m(2m-3)>=0
=>m>=3/2 hoặc m<=0

Ptr có nghiệm `<=>\Delta' >= 0`
`<=>(-m)^2-(-m) >= 0`
`<=>m(m+1) >= 0`
`<=>` $\left[\begin{matrix} m \le -1\\ m \ge 0\end{matrix}\right.$
`=>` Áp dụng Viét có:`{(x_1+x_2=[-b]/a=2m),(x_1.x_2=c/a=-m):}`
Ta có:`x_1 ^2+2mx_2+19(m+1)=0`
`<=>x_1 ^2+(x_1+x_2)x_2+19(m+1)=0`
`<=>x_1 ^2+x_1.x_2+x_2 ^2+19(m+1)=0`
`<=>(x_1+x_2)^2-x_1.x_2+19(m+1)=0`
`<=>(2m)^2-(-m)+19m+19=0`
`<=>4m^2+10m+19=0`
Ptr có:`\Delta'=5^2-4.19=-51 < 0`
`=>` Ptr vô nghiệm
Vậy ko có gtr `m` t/m yêu cầu đề bài
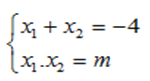

c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4
Theo Vi-et ta có: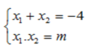
Ta có: x 1 2 + x 2 2 = 10 ⇔ x 1 + x 2 2 - 2x1x2 = 10
⇔ - 4 2 - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)
Vậy với m = 3 thì phương trình (1) có hai nghiệm thõa mãn: x 1 2 + x 2 2 = 10