Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

phương trình có a = 7 khác 0 => là phương trình bậc 2
vậy phương trình có nghiệm <=> \(\Delta'\ge0\Leftrightarrow\left(m-1\right)^2-7.\left(-m^2\right)\ge0\Leftrightarrow\left(m-1\right)^2+7m^2\ge0\)(thỏa mãn với mọi m)
b) theo vi et ta có
+) x1+x2 = -b/a = 2(m-1)/7
+) x1.x2 = c/a = -m2/7
a) Ta có : a = 7 ; b = 2(m-1) ; c = -m2
\(\Rightarrow\Delta'=\left(m-1\right)^2+7m^2\)
Do \(\left(m-1\right)^2\ge0\)mọi m và \(m^2\ge0\)mọi m
\(\Rightarrow\Delta'\ge0\)với mọi giá trị của m
Do đó PT có nghiệm với mọi giá trị của m
b) Gọi 2 nghiệm của PT là x1 ; x2
Theo định lí Vi-ét , ta có : \(\hept{\begin{cases}x_1+x_2=\frac{-2\left(m-1\right)}{7}\\x_1.x_2=\frac{-m^2}{7}\end{cases}}\)
Khi đó : \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2.x_1.x_2\)
\(=\left[\frac{-2\left(m-1\right)}{7}\right]^2-2.\frac{-m^2}{7}\)
\(=\frac{4\left(m-1\right)^2}{49}+\frac{2m^2}{7}\)
\(=\frac{4m^2-8m+4+14m^2}{49}\)
\(=\frac{18m^2-8m+4}{49}\)

a) Ta có: a = 7, b= 2(m-1), c = - m 2
Suy ra: Δ ' = ( m - 1 ) 2 + 7 m 2
Do ( m - 1 ) 2 ≥ 0 mọi m và m 2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
b) Gọi hai nghiệm của phương trình là x 1 ; x 2 .
Theo định lý Vi-et ta có: 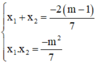
Khi đó:
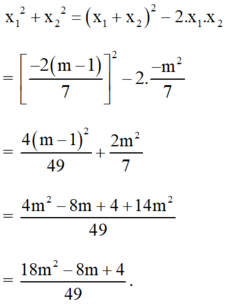

Gọi hai nghiệm của phương trình là x1; x2.
Theo định lý Vi-et ta có: 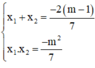
Khi đó:
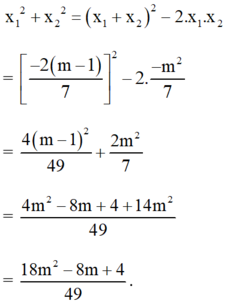

\(x^2+2\left(2m-1\right)x+3\left(m^2-1\right)=0\)
\(a,\) Để pt có nghiệm thì \(\Delta\ge0\)
\(\Rightarrow\left[2\left(2m-1\right)\right]^2-4\left[3\left(m^2-1\right)\right]\ge0\)
\(\Rightarrow4\left(4m^2-4m+1\right)-4\left(3m^2-3\right)\ge0\)
\(\Rightarrow16m^2-16m+4-12m^2+12\ge0\)
\(\Rightarrow4m^2-16m+16\ge0\)
\(\Rightarrow\left(2m-4\right)^2\ge0\)
Vậy pt có nghiệm với mọi m.
b, Theo viét : \(\left\{{}\begin{matrix}x_1+x_2=-2\left(2m-1\right)\\x_1x_2=3\left(m^2-1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=-4m+2\\x_1x_2=3m^2-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{-2+x_1+x_2}{4}\\x_1x_2=3\left(\dfrac{-2+x_1+x_2}{4}\right)^2-3\end{matrix}\right.\)
Vậy......

Vì phương trình đã cho là phương trình bậc hai nên để pt đã cho có nghiệm buộc \(\Delta\)'\(\ge\)0
\(\Leftrightarrow\left(-m-4\right)^2-\left(2m-1\right)\left(5m+2\right)\ge0\)
\(\Leftrightarrow-9m^2+9m+17\ge0\)
Tới đây mình bấm máy tính fx 570vn thì ra còn ai rảnh thì xài bảng xét dấu
\(\Leftrightarrow\dfrac{3-\sqrt{77}}{6}\le m\le\dfrac{3+\sqrt{77}}{6}\)
Vậy với .....
b, Theo hệ thức Vi-ét ta có :
\(\left\{{}\begin{matrix}S=x_1+x_2=-\dfrac{b}{a}=\dfrac{2\left(m+4\right)}{2m-1}\\P=x_1.x_2=\dfrac{c}{a}=\dfrac{5m+2}{2m-1}\end{matrix}\right.\)
c,Từ \(S=\dfrac{2m+8}{2m-1}\Leftrightarrow S=1+\dfrac{9}{2m-1}\\ \Leftrightarrow\left(S-1\right)\left(2m-1\right)=9\\ \Leftrightarrow2m-1=\dfrac{9}{S-1}\\ \Leftrightarrow m=\dfrac{S+8}{2S-2}\)
Thay \(m=\dfrac{S+8}{2S-2}\) vào \(P=\dfrac{5m+2}{2m-1}\) ta được:
\(P=\dfrac{7S+6}{18}\)
\(\Leftrightarrow18P=7S+6\)
Hay \(18x_1x_2=x_1+x_2+6\)
Vậy ....

- \(\Delta^'=m^2-\left(m-1\right)\left(m+1\right)=m^2-m^2+1=1>0\)vậy phương trình luôn có hai nghiệm với mọi \(m\ne1\)
- Theo viet ta có : \(\hept{\begin{cases}x_1+x_2=2m\\x_1x_2=m+1\end{cases}}\)\(\Rightarrow m+1=5\Rightarrow m=4\Rightarrow x_1+x_2=2m=2.4=8\)
- từ hệ thức viet ta khử m được hệ thức liên hệ giữa 2 nghiệm ko phụ thuộc m: thấy \(x_1+x_2-2x_2x_1=2m-2\left(m+1\right)=-2\)
- \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=-\frac{5}{2}\Leftrightarrow\frac{x_1^2+x_2^2}{x_1x_2}=-\frac{5}{2}\Leftrightarrow\frac{\left(x_1+x_2\right)^2-2x_1x_2}{x_1x_2}=-\frac{5}{2}\)\(\Leftrightarrow\frac{4m^2-2m-2}{m+1}=-\frac{5}{2}\Rightarrow8m^2-4m-4=-5m-5\left(m\ne-1\right)\)\(\Leftrightarrow8m^2+m+1=0\left(vn\right)\)không có giá trị nào của m thỏa mãn

Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
\(x^2_1+x^2_2=\left(x_1+x_2\right)^2-2x_1x_2\\ =\left[\dfrac{-2\left(m-1\right)^2}{7}\right]-2\dfrac{\left(-m\right)^2}{7}\\ =\dfrac{4m^2-8m+4}{49}+\dfrac{2m^2}{7}\\ =\dfrac{4m^2-8m+4+14m^2}{49}\\ =\dfrac{18m^2-8m+4}{49}\)
Vậy \(x^2_1+x^2_2=\dfrac{18m^2-8m+4}{49}\).
Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
x\(\dfrac{1}{2}\)+x\(\dfrac{2}{2}\)=(x1+x2)2−2x1x2
=[\(\dfrac{-2\left(m-1\right)^2}{7}\)]-2\(\dfrac{\left(-m\right)^2}{7}\)
=\(\dfrac{4m^2-8m+4}{49}\)+\(\dfrac{2m^2}{7}\)
=\(\dfrac{4m^2-8m+4+14m^2}{49}\)
=\(\dfrac{18m^2-8m+4}{49}\)
vậy x\(\dfrac{2}{1}\)+x\(\dfrac{2}{2}\)=\(\dfrac{18m^2-8m+4}{49}\)