Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: 2x-3y=5
=>3y=2x-5
=>\(y=\dfrac{2}{3}x-\dfrac{5}{3}\)
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{2}{3}x-\dfrac{5}{3}\end{matrix}\right.\)
Biểu diễn tập nghiệm:
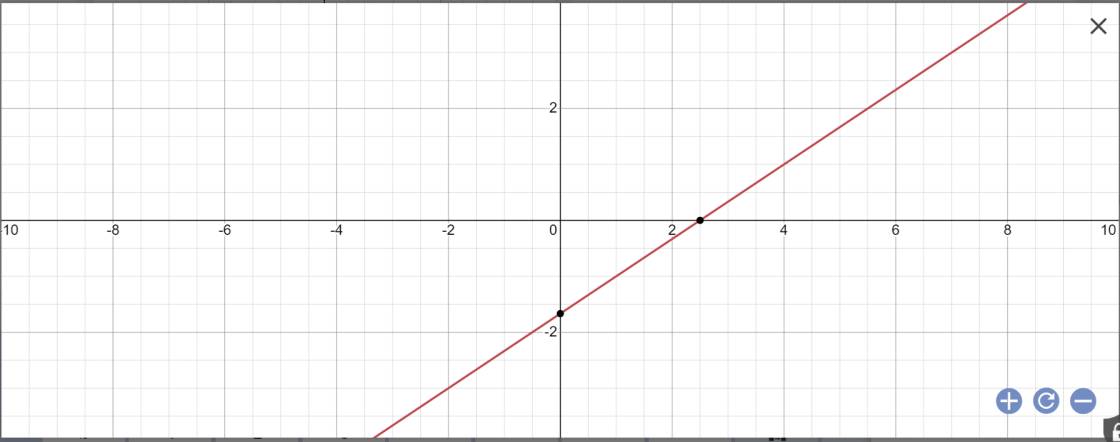
b: 4x+0y=12
=>4x=12
=>x=3
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x=3\\y\in R\end{matrix}\right.\)
Biểu diễn tập nghiệm:
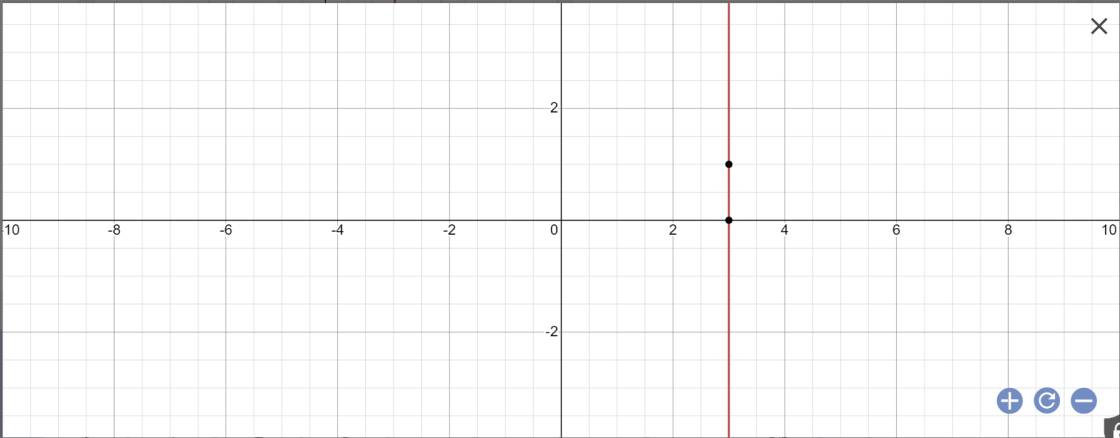
c: 0x-3y=6
=>-3y=6
=>y=-2
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=-2\end{matrix}\right.\)
Biểu diễn tập nghiệm:
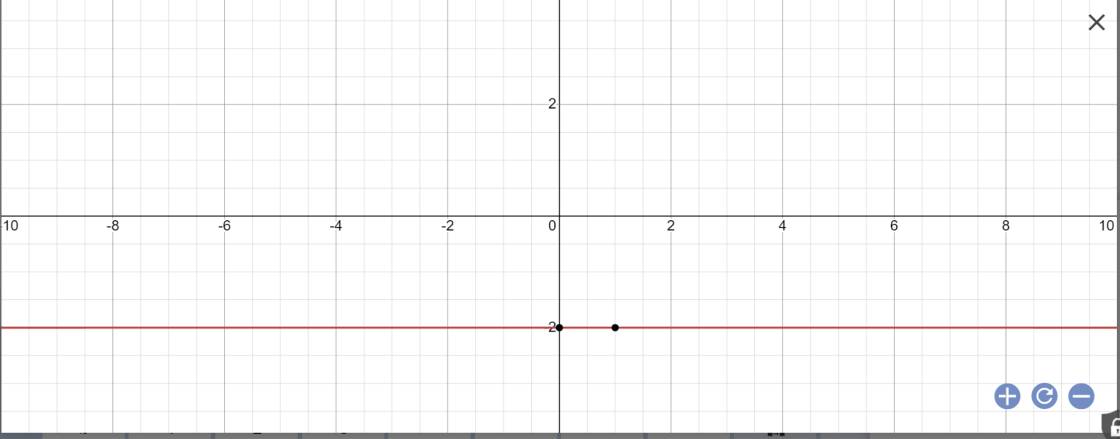
a) + Xét phương trình 2x + y = 4 (1) ⇔ y = -2x + 4
Vậy phương trình (1) có nghiệm tổng quát là (x ; -2x + 4) (x ∈ R).
+ Xét phương trình 3x + 2y = 5 (2) ⇔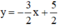 
Vậy phương trình (2) có nghiệm tổng quát là :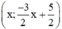 
(x ∈ R).
b) Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng (d) : y = -2x + 4.
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
Đường thẳng biểu diễn tập nghiệm của phương trình (2) là đường thẳng (d’) :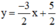 
Chọn x = 0 ⇒ y = 2,5.
Chọn y = 0 ⇒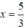 
⇒ (d’) đi qua hai điểm (0; 2,5) và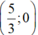 
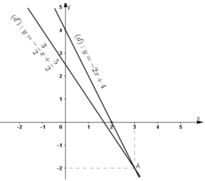
Hai đường thẳng cắt nhau tại A(3; -2).
Vậy (3; -2) là nghiệm chung của hai phương trình (1) và (2).
a: =>2x=y+3
=>x=(y+3)/2
Vậy: Nghiệm tổng quát là:
\(\left\{{}\begin{matrix}y\in R\\x=\dfrac{y+3}{2}\end{matrix}\right.\)
a) . Do đó phương trình có nghiệm dạng tổng quát như sau:
hoặc
b) Vẽ (d1): 2x + y = 4
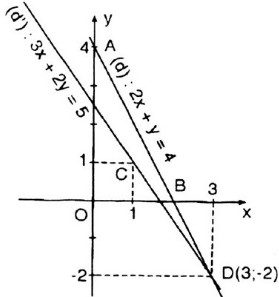
- Cho x = 0 => y = 4 được A(0; 4).
- Cho y = 0 => x = 2 được B(2; 0).
Vẽ (d2): 3x + 2y = 5
- Cho x = 0 => y = 
được C(0; ).
- Cho y = 0 => x = 
được D(; 0).
Hai đường thẳng cắt nhau tại M(3; -2).
Thay x = 3, y = -2 vào từng phương trình ta được:
2 . 3 + (-2) = 4 và 3 . 3 + 2 . (-2) = 5 (thỏa mãn)
Vậy (x = 3; y = -2) là nghiệm chung của các phương trình đã cho.
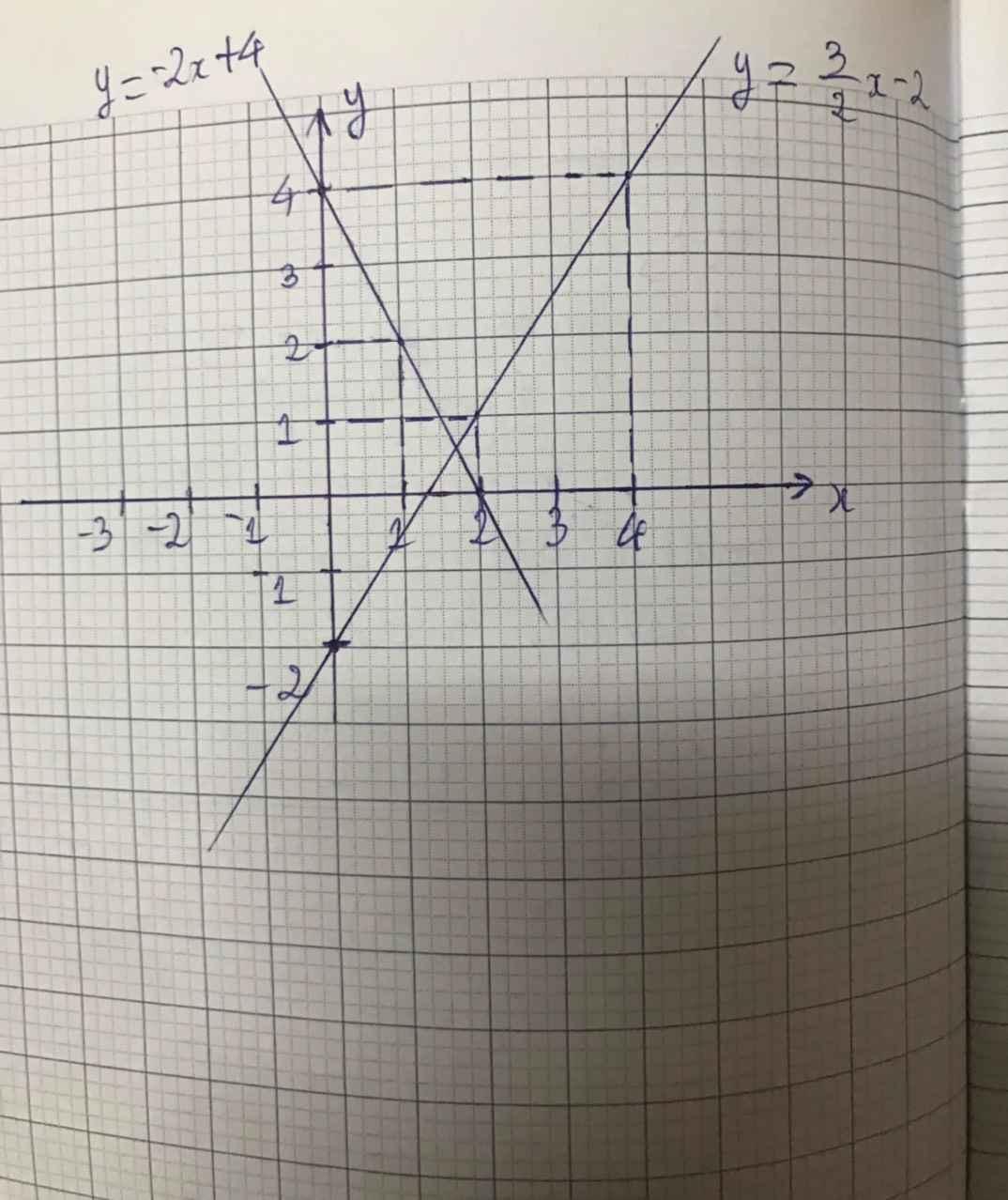
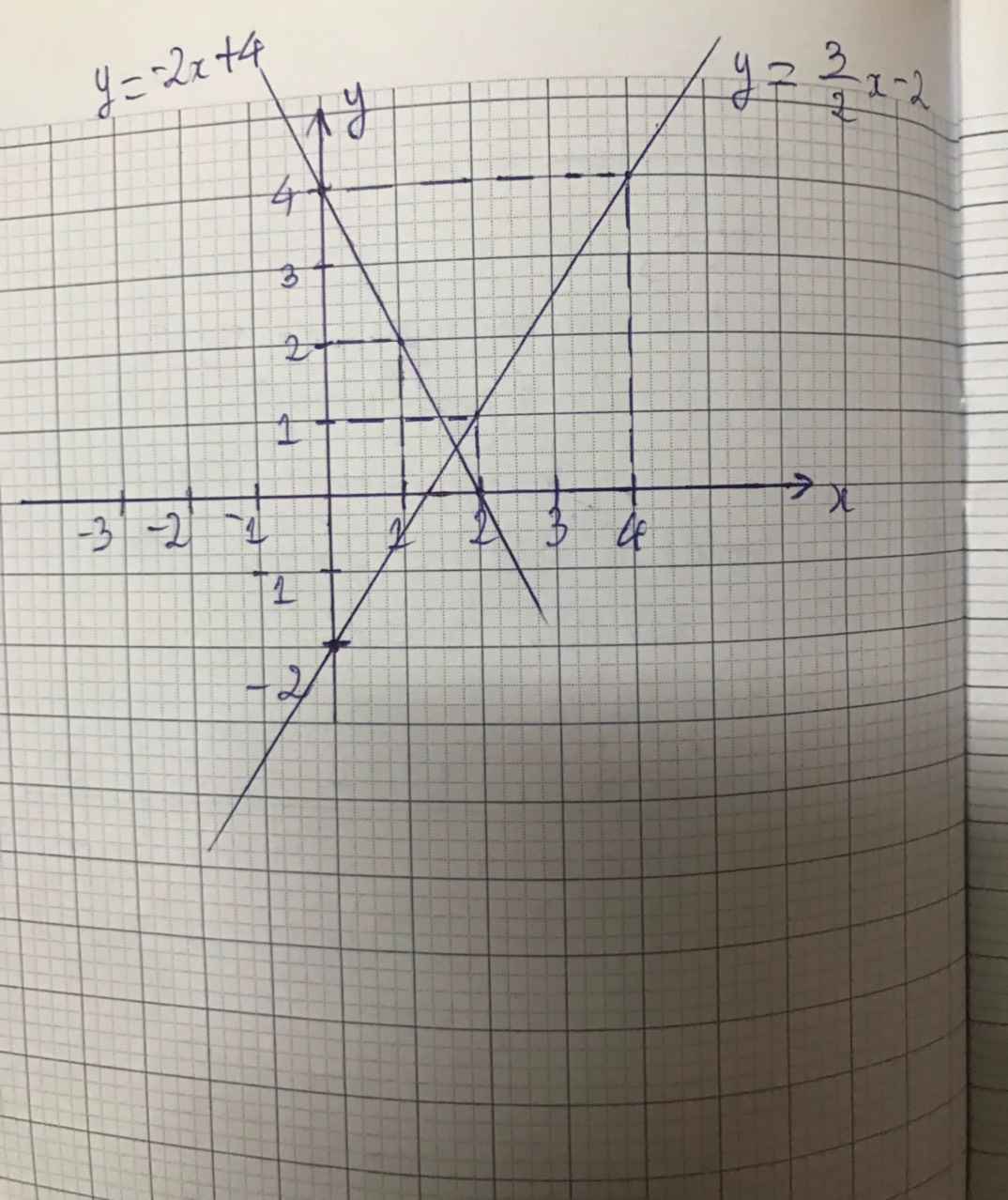
Sửa thành 2x + y = 4 cho dễ hơn tí nhé :Vvv
+ Xét phương trình 2x + y = 4 (1) <=> y = -2x + 4
Vậy phương trình (1) có nghiệm tổng quát là \(\left(x;-2x+4\right)\left(x\in R\right)\)
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng (d) : y = -2x + 4.
Chọn x = 0 => y = 4
Chọn y = 0 => x = 2.
=> (d) đi qua hai điểm (0 ; 4) và (2 ; 0)
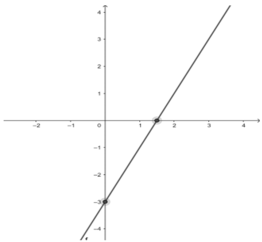
Phương trình tập nghiệm trên mặt phẳng tọa độ :