Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp: Sử dụng định luật bảo toàn động lượng.
Cách giải: Ta có thể biểu diễn các vecto động lượng như hình vẽ:
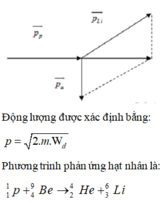
Áp dụng định luật bảo toàn động lượng cho hệ hai hạt p và Be.
![]()
Gọi góc giữa vec to động lượng của Li và vecto tổng động lượng là α. Ta có
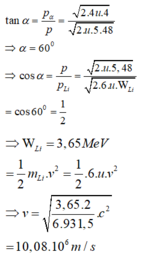
Đáp án A

\(_1^1p + _3^7 Li \rightarrow 2_2^4He\) => X là Heli.
Áp dụng định luật bảo toàn động lượng trước và sau phản ứng
\(\overrightarrow P_{p} = \overrightarrow P_{He_1} + \overrightarrow P_{He_2}\) , do \( (\overrightarrow P_{Li} = \overrightarrow 0)\)
Dựa vào hình vẽ ta có
\(P_p^2 + P_{He_1}^2 - 2P_pP_{He_1} \cos {60^o}= P_{He_2}^2\)
Mà \(P_{He_1} = P_{He_2}\)
=> \(P_p^2 - 2P_pP_{He} \cos {60^o}= 0\)
=> \(P_p^2 =2P_pP_{He} \cos {60^o}\)
=> \(P_p =P_{He} \)
=> \(m_pv_p=m_{He}v_{He} \)
=> \(\frac{v_p}{v_{He}} = 4.\)

\(_1^1p + _4^9Be \rightarrow _2^4He + _3^6X\)
Áp dụng định luật bảo toàn động lượng \(\overrightarrow P_p=\overrightarrow P_{He}+ \overrightarrow P_{X} \) (do hạt Be đứng yên)
Dựa vào hình vẽ ta có \(P_{p}^2+ P_{He}^2 = P_X^2\)
=> \(2m_{p}K_{p}+2m_{He} K_{He} = 2m_{X}K_{X}. \)
=> \(K_{p}+4K_{He} = 6K_{X} => K_X = 6MeV.\)

Chọn đáp án D.
Số prôtôn và nơtron của hạt nhân X lần lượt là 8 và 9.

Chọn đáp án D.
Số prôtôn và nơtron của hạt nhân X lần lượt là 8 và 9

Chọn đáp án D.
Số prôtôn và nơtron của hạt nhân X lần lượt là 8 và 9.

Chọn đáp án D.
Số prôtôn và nơtron của hạt nhân X lần lượt là 8 và 9.