BT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
8 tháng 10 2023
Lời giải:
a. $A=9x^2+15x+6xy+y^2+5y=(9x^2+6xy+y^2)+(15x+5y)$
$=(3x+y)^2+5(3x+y)=0^2+5.0=0$
b. $25x^2-y^4-5x+y^2=(25x^2-y^4)-(5x-y^2)=(5x-y^2)(5x+y^2)-(5x-y^2)$
$=(5x-y^2)(5x+y^2-1)$
CM
31 tháng 1 2019
a) Đa thức thương x 2 – 6x + 9.
b) Đa thức thương 2 x 2 – 5.
c) Đa thức thương x 2 + 4x + 3 và đa thức dư -12.
d) Đa thức x + 5 và đa thức dư x – 4.
B
23 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
UB
1
TA
20 tháng 7 2021
`5x(4x^2-2x+1)-2x(10x^2-5x-2)`
`= 20x^3-10x^2+5x - (20x^3-10x^2-4x)`
`=9x`
Thay `x=15` có: `9.15=135`.
20 tháng 10 2021
\(a,\Leftrightarrow\left(x-4\right)\left(x^2+5\right)>0\\ \Leftrightarrow x-4>0\left(x^2+5\ge5>0\right)\\ \Leftrightarrow x>4\\ b,\Leftrightarrow\left(x-y\right)\left(3x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=y\left(vô.lí.do.x\ne y\right)\\x=\dfrac{5}{3}\left(tm\right)\end{matrix}\right.\\ \Leftrightarrow S=x^2-x=\dfrac{25}{9}-\dfrac{5}{3}=\dfrac{10}{9}\)
PT
1
CM
20 tháng 3 2018
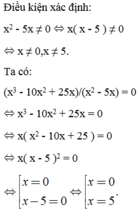
So sánh điều kiện, không có giá trị nào của x thỏa mãn.
Vậy không có giá trị x nào thỏa mãn yêu cầu đề bài.
27 tháng 7 2021
Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)
P=(3x^2+15x-6)/(9x^2-1)
=[-3(9x^2-1)+30x^2+15x-9]/(9x^2-1)
=-3(9x^2-1)/(9x^2-1) + (30x^2+15x-9)/(9x^2-1)
=-3 + 3(10x^2+5x-3)/(9x^2-1)
=-3 + 0 =-3 (do 10x^2+5x-3=0)