Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

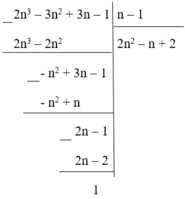
2 n 3 – 3 n 2 + 3n – 1 = (2 n 2 – n + 2)(n – 1) + 1
Để 2 n 3 – 3 n 2 + 3n – 1 chia hết cho n – 1 thì 1 chia hết cho n – 1
=> (n – 1) Є {1;-1}
n – 1 1 -1
n 2 0
P 9 1
TM TM
Vậy n Є {0; 2} để P Є Z
Đáp án cần chọn là: A

Ta có
a x 2 – 5 x 2 – a x + 5 x + a – 5 = x 2 a – 5 – x a – 5 + a – 5 = a – 5 x 2 – x + 1
Suy ra m = -5; n = 1
Đáp án cần chọn là: D

Ta có
x 2 – 4 x y + 4 y 2 – 4 = x 2 – 2 . x . 2 y + 2 y 2 – 4 = x – 2 y 2 – 2 2 = x – 2 y – 2 x – 2 y + 2
Vậy m = 2.
Đáp án cần chọn là: B

Ta có
M = ( x 4 y n + 1 - 1 2 x 3 y n + 2 ) : ( 1 2 x 3 y n ) - 20 x 4 y : 5 x 2 y = ( x 4 y n + 1 : 1 2 x 3 y n ) - ( 1 2 x 3 y n + 2 ) : ( 1 2 x 3 y n ) - 4 x 2 = 2 x 4 - 3 y n + 1 - n – x 3 - 3 y n + 2 - n – 4 x 2 = 2 x y – y 2 – 4 x 2 = - y 2 – 2 x y + x 2 + 3 x 2 = - [ ( x – y ) 2 + 3 x 2 ]
Vì với x;y ≠ 0 thì ( x – y ) 2 + 3 x 2 > 0 nên - [ ( x – y ) 2 + 3 x 2 ] < 0 ; Ɐ x;y ≠ 0
Hay giá trị của M luôn là số âm
Đáp án cần chọn là: A

Ta có
x 2 – 4 y 2 – 2 x – 4 y = x 2 – 4 y 2 – 2 x + 4 y = x – 2 y x + 2 y – 2 x + 2 y = x + 2 y x – 2 y – 2
Suy ra m = -2
Đáp án cần chọn là: A

Ta có
( 4 x 2 + 4 x – 3 ) 2 – ( 4 x 2 + 4 x + 3 ) 2 = ( 4 x 2 + 4 x – 3 + 4 x 2 + 4 x + 3 ) ( 4 x 2 + 4 x – 3 – 4 x 2 – 4 x – 3 ) = ( 8 x 2 + 8 x ) . ( - 6 )
= 8.x(x + 1).(-6)
= -48x(x + 1) nên m = -48 < 0
Đáp án cần chọn là: B

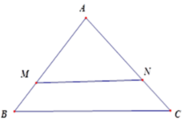
Vì MN // BC => tam giác AMN đồng dạng với tam giác ABC
Đáp án: C

a:
\(\dfrac{3\left(2x+1\right)}{4}-5-\dfrac{3x+2}{10}=\dfrac{2\left(3x-1\right)}{5}\)
\(\Leftrightarrow\dfrac{15\left(2x+1\right)-100-2\left(3x+2\right)}{20}=\dfrac{8\left(3x-1\right)}{20}\)
\(\Leftrightarrow15\left(2x+1\right)-100-2\left(3x+2\right)=8\left(3x-1\right)\)
\(\Leftrightarrow30x+15-100-6x+4=24x-8\)\(\Leftrightarrow30x-6x-24x=100-4-8\)
\(\Leftrightarrow0x=88\)
Vậy pt vô nghiệm
b:
\(\dfrac{x-15}{23}+\dfrac{x-23}{15}-2=0\)
\(\Leftrightarrow\dfrac{x-15}{23}+\dfrac{x-23}{15}=2\)
\(\Leftrightarrow\dfrac{x-15}{23}-1+\dfrac{x-23}{15}-1=2-2\)
\(\Leftrightarrow\dfrac{x-15-23}{23}+\dfrac{x-23-15}{15}=0\)
\(\Leftrightarrow\dfrac{x-38}{23}+\dfrac{x-23}{15}=0\)
\(\Leftrightarrow\left(x+38\right)\left(\dfrac{1}{23}+\dfrac{1}{15}\right)=0\)
Vì \(\dfrac{1}{23}+\dfrac{1}{15}\ne0\) nên x + 38 =0 \(\Leftrightarrow x=-38\)
Vậy tập nghiện của pt S= {-38}
c:
\(\dfrac{3\left(2x+1\right)}{4}-\dfrac{5x+3}{6}+\dfrac{x+1}{3}=x+\dfrac{7}{12}\)
\(\Leftrightarrow\dfrac{9\left(2x+1\right)-2\left(5x+3\right)+4\left(x+1\right)}{12}=\dfrac{12x+7}{12}\)
\(\Leftrightarrow9\left(2x+1\right)-2\left(5x+3\right)+4\left(x+1\right)=12x+7\)
\(\Leftrightarrow18x+9-10x-6+4x+4=12x+7\)
\(\Leftrightarrow18x-10x+4x-12x=7-9+6-4\)
\(\Leftrightarrow0x=0\)
Vậy pt vô số nghiệm

Theo câu 17, ta có P = - 3 x + 7 x + 4
Nên ta có:
Đáp án cần chọn là: A