Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Vì \(CE\perp MA\)tại E (gt) => \(\widehat{AEC}=90^o\)
\(CD\perp AB\)tại D=> \(\widehat{ADC}=90^o\)
Xét tứ giác AECD có: \(\widehat{AEC}+\widehat{ADC}=90^o+90^o=180^o\)=> AECD là tứ giác nội tiếp đt \((G,R=\frac{AC}{2})\)trong đó G là trung điểm của AC (dhnb)
Cmtt ta có: BFCD là tứ giác nội tiếp đt \((H,R=\frac{BC}{2})\)trong đó H là trung điểm của BC
b.
Vì AECD là tứ giác nội tiếp (cmt) => \(\widehat{EAC}=\widehat{EDC}\)(2 góc nội tiếp cùng chắn \(\widebat{EC}\)) (1)
Do MA là tiếp tuyến của đt(O) (gt)=> \(\widehat{EAC}=\frac{1}{2}sđ\widebat{AC}\)(t/c góc tạo bởi tiếp tuyến và dây cung)
Xét đt (O) có: \(\widehat{ABC}=\widehat{DBC}=\frac{1}{2}sđ\widebat{AC}\)(t/c góc nội tiếp) => \(\widehat{EAC}=\widehat{DBC}\)(2)
vì BFCD là tứ giác nội tiếp => \(\widehat{DBC}=\widehat{DFC}\)(2 góc nội tiếp cùng chắn \(\widebat{DC}\)) (3)
Từ (1),(2) và (3) => \(\widehat{EDC}=\widehat{DFC}\)
do AECD là tứ giác nội tiếp (cmt) => \(\widehat{CED}=\widehat{CAD}\)(2 góc nội tiếp cùng chắn \(\widebat{CD}\)) (4)
Vì MB là tiếp tuyến của đt (O) tại B (gt) => \(\widehat{CBF}=\frac{1}{2}sđ\widebat{BC}\)(T/c góc tạo bởi tiếp tuyến và dây cung)
Xét đt (O) có: \(\widehat{BAC}=\widehat{DAC}=\frac{1}{2}sđ\widebat{BC}\)(t/c góc nội tiếp) => \(\widehat{CBF}=\widehat{DAC}\)(5)
lại có: BFCD là tứ giác nội tiếp (cmt) => \(\widehat{CBF}=\widehat{CDF}\)(2 góc nội tiếp cùng chắn \(\widebat{CF}\)) (6)
Từ (4), (5) và (6) => \(\widehat{CED}=\widehat{CDF}\)
Xét \(\Delta ECD\)và \(\Delta DCF\)có:
\(\widehat{CED}=\widehat{CDF}\)(Cmt)
\(\widehat{EDC}=\widehat{DFC}\)(Cmt)
=> \(\Delta ECD~\Delta DCF\)(g.g) => \(\frac{EC}{DC}=\frac{CD}{CF}\Rightarrow CD^2=CE\times CF\)(Đpcm)
c. Vì I là giao điểm của AC và DE (gt) => \(I\in AC\)
K là giao điểm của BC và DF (gt) => \(K\in BC\)
=> \(\widehat{ICK}=\widehat{ACB}\)
Vì \(\widehat{EDC}=\widehat{ABC}\left(cmt\right)\Rightarrow\widehat{IDC}=\widehat{ABC}\left(do\overline{E,I,D}\Rightarrow\widehat{EDC}=\widehat{IDC}\right)\)
\(\widehat{CDF}=\widehat{BAC}\left(cmt\right)\Rightarrow\widehat{CDK}=\widehat{BAC}\left(do\overline{F,K,D}\Rightarrow\widehat{CDF}=\widehat{CDK}\right)\)
Xét tứ giác ICKD có : \(\widehat{ICK}+\widehat{IDK}=\widehat{ICK}+\widehat{IDC}+\widehat{CDK}=\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\)
(Áp dụng định lý tổng 3 góc trong \(\Delta ABC\)ta có: \(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\))
=> Tứ giác ICKD là tứ giác nội tiếp (dhnb) => 4 điểm I,C,K,D cùng thuộc 1 đường tròn (đpcm)
d. Vì ICKD là tứ giác nội tiếp (cmt) => \(\widehat{CIK}=\widehat{CDK}\)(2 góc nội tiếp cùng chắn \(\widebat{CK}\))
Lại có: \(\widehat{CDK}=\widehat{BAC}\)(Cmt) => \(\widehat{CIK}=\widehat{BAC}\)mà 2 góc này ở vị tri đồng vị => IK // AB (Dhnb)
Do \(CD\perp AB\left(gt\right)\)=> \(IK\perp CD\)(Quan hệ tính vuông góc và tính song song của 3 đt)

câu a bạn tự làm nha b)xét đường tròn ngoại tiếp tứ giác ADCE góc CDE =góc CAE (2 góc nt cùng chắn cung EC) mà góc CBA = góc CAE ( goc nt và goc tạo bởi tia tiếp tuyến và dây cg cùng chắn cg AC ) suy ra gócCDE = góc CBE c) cm tứ giác BDCF nội tiếp suy ra góc CDF = góc CBF mà góc CAB = góc CBF do đó góc cab = góc cdf cm tt góc CDE = góc CBA TA CÓ : CDE +CDF = CAB+CBA =90 ĐỘ ( VÌ tam giác acb vuông tại c ) xét tứ giác CIDK có ICK +IDK =180 độ mà ICK và IDK là 2 góc đối nhau suy ra tứ giác CIDK nt nên CKI = CDI ( 2goc nt chắn cg IC) mà CDE = CBA nên CKI = CBA DO ĐÓ : IK //AB

1) Hình vẽ câu 1) đúng
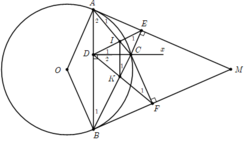
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B

gọi G là giao của tia đối tia CD với AM (ta giả sử cung AC < cung BC)
ý c: từ b suy ra tam giác CDE đồng dạng CFD
=> \(\widehat{ECD}=\widehat{FCD}\)
ta có: \(\widehat{ECD}+\widehat{GCE}=180^o\)
\(\widehat{FCD}+\widehat{GCF}=180^o\)
\(\widehat{GCE}=\widehat{GCF}\)suy ra đccm
ý d: CM IK//AB
Ta có: \(\widehat{FDB}=\widehat{FCB}\)(BDCF nôi tiếp đường tròn)
\(\hept{\begin{cases}\widehat{FCB}+\widehat{FBC}=90^o\\\widehat{DCA}+\widehat{CAD}=90^o\end{cases}}\)
mà \(\widehat{CAD}=\widehat{FBC}\)(cùng chắn cung BC)
\(\Rightarrow\widehat{FCB}=\widehat{DCA}\Rightarrow\widehat{FDB}=\widehat{DCA}\)(1)
Tương tự:
\(\hept{\begin{cases}\widehat{ECA}+\widehat{EAC}=90^o\\\widehat{DCB}+\widehat{DBC}=90^o\end{cases}}\)
mà \(\widehat{EAC}=\widehat{DBC}\)(cùng chắn cung AC)
\(\Rightarrow\widehat{ECA}=\widehat{DCB}\). mà \(\widehat{ECA}=\widehat{EDA}\)(tứ giác ECDA nội tiếp nên 2 góc kia cùng chắn cung AE)
\(\Rightarrow\widehat{DCB}=\widehat{EDA}\)(2)
(1)+(2) => \(\widehat{ACD}+\widehat{BCD}=\widehat{FDB}+\widehat{EDA}\)
\(\Rightarrow\widehat{ICK}=\widehat{FDB}+\widehat{EDA}\)\(\Rightarrow\widehat{ICK}+\widehat{IDK}=\widehat{FDB}+\widehat{EDA}+\widehat{IDK}=180^o\)
suy ra tứ giác IDKC nội tiếp \(\Rightarrow\widehat{CKI}=\widehat{CDI}=\widehat{CAE}=\widehat{CBA}\)
mà góc CKI và góc CBA ở vị trí đồng vị suy ra IK//AB. ta đc đccm.
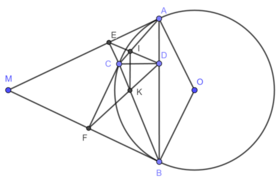

a) Xét tứ giác AECD có \(\widehat{CDE}+\widehat{CEA}=90^0+90^0=180^0\Rightarrow\)tứ giác AECD nội tiếp
b) Xét đường tròn (O) có MA là tiếp tuyến\(\Rightarrow\widehat{EAC}=\widehat{CBA}\)(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(\stackrel\frown{AC}\)) (1)
Ta lại có tứ giác AECD nội tiếp\(\Rightarrow\widehat{EAC}=\widehat{CDE}\)(2 góc nội tiếp cùng chắn cung \(\stackrel\frown{CE}\)) (2)
Từ (1),(2)\(\Rightarrow\widehat{CDE}=\widehat{CBA}\)
c)
Xét tứ giác BFCD có\(\widehat{BFC}+\widehat{BDC}=90^0+90^0=180^0\Rightarrow\) tứ giác BFCD nội tiếp\(\Rightarrow\) \(\widehat{DBF}+\widehat{DCF}=180^0\)
Ta lại có tứ giác AECD nội tiếp\(\Rightarrow\widehat{DCE}+\widehat{DAE}=180^0\)
Mà \(\widehat{DBF}=\widehat{DAE}\)
Suy ra \(\widehat{DCE}=\widehat{DCF}\Rightarrow\widehat{DCA}+\widehat{ECA}=\widehat{BCD}+\widehat{BCF}\Rightarrow\widehat{DCA}+\widehat{EDA}=\widehat{BCD}+\widehat{BCF}\Rightarrow\left(90^0-\widehat{DBC}\right)+\widehat{EDA}=\left(90^0-\widehat{CDE}\right)+\widehat{BCF}\Rightarrow\widehat{EDA}=\widehat{BCF}\)
Xét tứ giác CKDI có\(\widehat{KCI}+\widehat{KDI}=\widehat{KCD}+\widehat{ICD}+\widehat{KDC}+\widehat{CDI}=\widehat{KCD}+\widehat{KCF}+\widehat{FBC}+\widehat{CBD}=\widehat{DBF}+\widehat{FCD}=180^0\)\(\Rightarrow\)tứ giác CKDI nội tiếp\(\Rightarrow\widehat{CDI}=\widehat{CKI}\)
Mà \(\widehat{CDI}=\widehat{CBD}\)
Suy ra \(\widehat{CKI}=\widehat{CBD}\Rightarrow\)IK//AB