Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

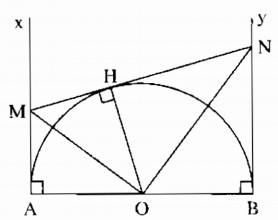
a) Gọi I là tiếp điểm của tiếp tuyến MN với đường tròn (O). Nối OI.
Ta có: ˆAOI+ˆBOI=180∘AOI^+BOI^=180∘ (hai góc kề bù)
OM là tia phân giác cảu góc AOI (tính chất hai tiếp tuyến cắt nhau)
Quảng cáo
ON là tia phân giác của góc BOI (tính chất hai tiếp tuyến cắt nhau)
Suy ra: OM ⊥ ON (tính chất hai góc kề bù)
Vậy ˆMON=90∘MON^=90∘
b) Ta có: MA = MI (tính chất hai tiếp tuyến cắt nhau)
NB = NI (tính chất hai tiếp tuyến cắt nhau)
Mà: MN = MI + IN
Suy ra: MN = AM + BN
c) Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến) theo hệ thức lượng trong tam giác vuông, ta có:
OI2=MI.NIOI2=MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra: AM.BN=OI2=R2AM.BN=OI2=R2.
good luck!

Mấy bữa nay mình ghét nhất là từ chtt ấy nha câu dễ thì có trong đó nhưng những câu khó tất nhiên ko có rồi mình mong các bạn hỉu ý của mình và ai biết thì làm bài giải đầy đủ sẽ có nhìu người tick chứ cứ chtt hoài mình muốn chết còn sướng hơn các bạn thử nghĩ nếu như một lúc nào đó các bạn có bài giải rất khó nhưng ko biết làm rồi lên đây hỏi mà ai cũng trả lời là chtt các bạn có bực mình ko. Mình chỉ nói thế thôi mong các bạn sẽ hỉu và đừng ghi chữ chtt nữa.

