Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

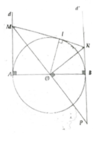
a, ∆MAO = ∆PBO => MO = OP => ∆MNP cân
Vì đường cao NO đồng thời là đường trung tuyến
b, 1 O I 2 - 1 O M 2 + 1 O N 2
= 1 O P 2 + 1 O N 2 = 1 O B 2 => OI = R
=> MN là tiếp tuyến của (O)
c, AM.BN = MI.IN = O I 2 = R 2
d, S A M N B = M N . A B 2
=> S A M N B min
<=> M N m i n <=> AM = R

O A B x y d M P N I
a/ Xét \(\Delta AOM\)và \(\Delta BOP\)có
\(\hept{\begin{cases}AO=BO\\\widehat{AOM}=\widehat{BOP}\\\widehat{OAM}=\widehat{OBP}=90\end{cases}}\)
\(\Rightarrow\Delta AOM=\Delta BOP\)
\(\Rightarrow OM=OP\)
Ta lại có ON vuông góc với MP
\(\Rightarrow ON\)vừa là đường cao vừa là đường trung tuyến nên \(\Delta MNP\) cân tại N
\(\Rightarrow\widehat{NMP}=\widehat{NPM}\)
b/ Xét \(\Delta OIN\)và \(\Delta OBN\)có
\(\hept{\begin{cases}ON\left(chung\right)\\\widehat{OIN}=\widehat{OBN}=90\\\widehat{ONI}=\widehat{ONB}\left(\widehat{ONI}+\widehat{OMN}=\widehat{ONB}+\widehat{OPN}=90\right)\end{cases}}\)
\(\Rightarrow\Delta OIN=\Delta OBN\)
\(\Rightarrow OI=ON=R\)
\(\Rightarrow MN\) là đường tuyeesp tuyến (O) tiếp điểm tại I
c/ Ta có \(\hept{\begin{cases}MI=AM\\NI=BN\end{cases}\left(1\right)}\)
Xét \(\Delta OIM\)và \(\Delta NIO\)có
\(\hept{\begin{cases}\widehat{OIM}=\widehat{NIO}=90\\\widehat{IMO}=\widehat{ION}\left(+\widehat{IOM}=90\right)\end{cases}}\)
\(\Rightarrow\Delta OIM\approx\Delta NIO\)
\(\Rightarrow\frac{OI}{NI}=\frac{MI}{OI}\Rightarrow MI.NI=OI^2=R^2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow AM.BN=R^2\)

Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')