Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

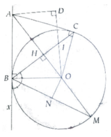
Cho đường tròn (O), đường kính AB. Trên tiếp tuyến của (O) tại A lấy điểm M (M khác A). Từ M kẻ cát tuyến MCD (C nằm ở giữa M và D; tia MC nằm giữa MA và MO) và tiếp tuyến thứ hai MI (I là tiếp điểm) với đường tròn (O). Đường thẳng BC và BD cắt đường thẳng OM lần lượt tại E và F. Chứng minh:
O là trung điểm của EF
a: OH*OA=OB^2=R^2
b: ΔOCD cân tại O
mà OM là trung tuyến
nên OM vuông góc với CD
Xét tứ giác OMBA có
góc OMA=góc OBA=90 độ
nên OMBA là tứ giác nội tiếp
c: Xét ΔOHE vuông tại H và ΔOMA vuông tại M có
góc MOA chung
Do đó: ΔOHE đồng dạng với ΔOMA
=>OH/OM=OE/OA
=>OM*OE=OH*OA=R^2=OC^2=OD^2
=>ΔODE vuông tại D
=>DE là tiếp tuyến của (O)

a: OH*OA=OB^2=R^2
b: ΔOCD cân tại O
mà OM là trung tuyến
nên OM vuông góc với CD
Xét tứ giác OMBA có
góc OMA=góc OBA=90 độ
nên OMBA là tứ giác nội tiếp
c: Xét ΔOHE vuông tại H và ΔOMA vuông tại M có
góc MOA chung
Do đó: ΔOHE đồng dạng với ΔOMA
=>OH/OM=OE/OA
=>OM*OE=OH*OA=R^2=OC^2=OD^2
=>ΔODE vuông tại D
=>DE là tiếp tuyến của (O)

a: Xét ΔOBA vuông tại B có BH là đường cao
nên OH*OA=OB^2=R^2
b: Xét ΔABC và ΔADB có
góc ABC=góc ADB
góc BAC chung
Do đó; ΔABCđồng dạng với ΔADB
=>AB/AD=AC/AB
=>AB^2=AD*AC
=>AD*AC=AH*AO

a, OH.OA = O B 2 = R 2 không đổi\
b, Chứng minh ∆ABO = ∆ACO
c, Vẽ ON ⊥ BM => B O N ^ = M O N ^
có B O N ^ = M B x ^ ; M O N ^ = H B M ^
=> M B x ^ = H B M ^
=> MB là phân giác của
C
B
x
^
nên M cách đều hai cạnh BA và BC mà AM là phân giác
B
A
C
^
=> đpcm
d, Ta có ∆ODA:∆OHI => OI.OD = OH.OA = R 2
Ta có: 3OI+OD ≥ 2 3 O I . O D = 2R 3
=> (3OI+OD)min = 2R 3 <=> OI = R 3 3

a: Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC tại trung điểm H của BC
Gọi K là giao điểm của OS và ED
Xét (O) có
SE,SD là các tiếp tuyến
Do đó: SE=SD
=>S nằm trên đường trung trực của ED(3)
Ta có: OE=OD
=>O nằm trên đường trung trực của ED(4)
Từ (3) và (4) suy ra SO là đường trung trực của ED
=>SO\(\perp\)ED tại trung điểm K của ED
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=R^2\left(5\right)\)
Xét ΔODS vuông tại D có DK là đường cao
nên \(OK\cdot OS=OD^2=R^2\left(6\right)\)
Từ (5) và (6) suy ra \(OH\cdot OA=OK\cdot OS\)
=>\(\dfrac{OH}{OK}=\dfrac{OS}{OA}\)
Xét ΔOHS và ΔOKA có
\(\dfrac{OH}{OK}=\dfrac{OS}{OA}\)
góc HOS chung
Do đó: ΔOHS đồng dạng với ΔOKA
=>\(\widehat{OHS}=\widehat{OKA}\)
=>\(\widehat{OHS}=90^0\)
=>HO\(\perp\)SH tại H
mà HO\(\perp\)BH tại H
và SH,BH có điểm chung là H
nên S,H,B thẳng hàng
mà H,B,C thẳng hàng
nên S,B,H,C thẳng hàng
=>S,B,C thẳng hàng

a: OH*OA=OB^2=R^2
b: ΔOCD cân tại O
mà OM là trung tuyến
nên OM vuông góc với CD
Xét tứ giác OMBA có
góc OMA=góc OBA=90 độ
nên OMBA là tứ giác nội tiếp
c: Xét ΔOHE vuông tại H và ΔOMA vuông tại M có
góc MOA chung
Do đó: ΔOHE đồng dạng với ΔOMA
=>OH/OM=OE/OA
=>OM*OE=OH*OA=R^2=OC^2=OD^2
=>ΔODE vuông tại D
=>DE là tiếp tuyến của (O)
a) Sửa đề: Chứng minh A,B,O,C cùng thuộc một đường tròn
Gọi D là trung điểm của AO
Ta có: ΔBOA vuông tại B(AB là tiếp tuyến của (O) có B là tiếp điểm)
mà BD là đường trung tuyến ứng với cạnh huyền OA(D là trung điểm của OA)
nên \(BD=\dfrac{OA}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(OD=DA=\dfrac{OA}{2}\)(D là trung điểm của OA)
nên BD=OD=DA(1)
Ta có: ΔOCA vuông tại C(CA là tiếp tuyến của (O) có C là tiếp điểm)
mà CD là đường trung tuyến ứng với cạnh huyền OA(D là trung điểm của OA)
nên \(CD=\dfrac{OA}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(OD=AD=\dfrac{OA}{2}\)(D là trung điểm của OA)
nên CD=OD=AD(2)
Từ (1) và (2) suy ra DB=DA=DC=DO
hay A,B,C,O cùng thuộc đường tròn (D)
b) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
hay A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Từ (3) và (4) suy ra AO là đường trung trực của BC
hay AO\(\perp\)BC(đpcm)
c) Áp dụng hệ thức lượng trong tam giác vuông vào ΔOBA vuông tại B có BH là đường cao ứng với cạnh huyền OA(BC\(\perp\)OA tại H), ta được:
\(OH\cdot OA=OB^2\)
mà OB=R(B\(\in\)(O;R))
nên \(OH\cdot OA=R^2\)
Vậy: \(OH\cdot OA=R^2\)