Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

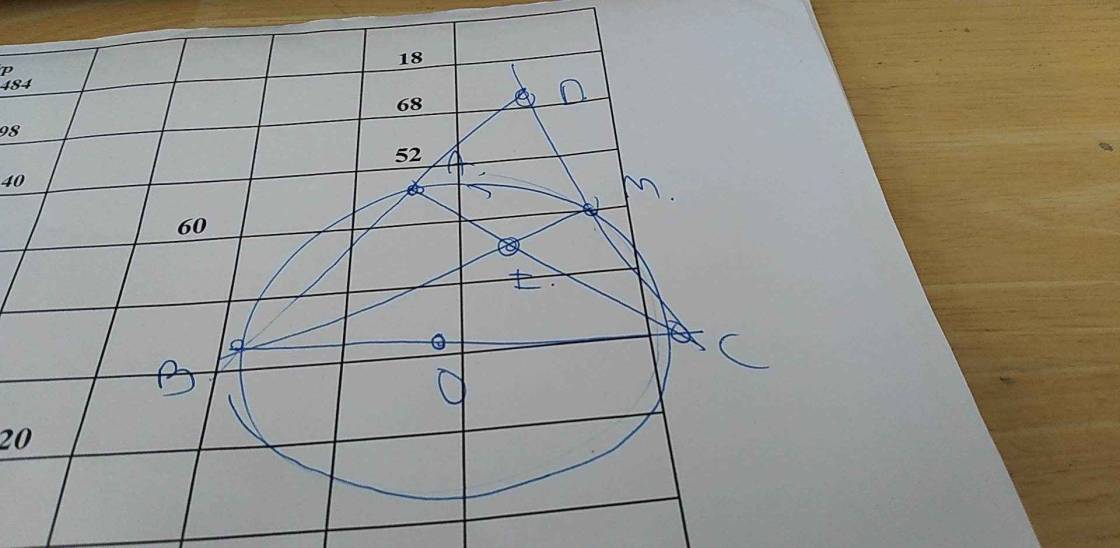
hình tự vẽ nha!
a) Ta có: OB=OA=AB=R nên ΔOAB đều.
b) ta có góc BMC=90⇒góc BMD=90 (kề bù)
xét ΔBMD có: \(\widehat{MBD}+\widehat{MDB}=90^O\)
do đó \(\widehat{MDB}\) = \(\widehat{AIB}\)
Vậy tứ giác AIMD nội tiếp đường tròn đường kính DI
c) ta có \(\widehat{ADI}=\widehat{AMI}\) (2 góc nội tiếp cùng chắn cung AI của đường tròn đường kính DI)
mà \(\widehat{AMB}=\widehat{ACB}\) ( 2 góc nội tiếp cùng chắn cung AB của đường tròn tâm O)
ΔABC vuông tại A, có \(\widehat{ABC}\)=60o⇒ \(\widehat{ACB}\) =30o
Vậy \(\widehat{ADI}\) =30o
d) vì \(\widehat{ABM}\) = 45o⇒ΔDMB vuông cân tại M. ta tính được MB= 2R.sin75o
⇒DB⇒AD=BD - AB

a: góc CAB=góc CMB=1/2*180=90 độ
=>CA vuông góc DB và BM vuông góc DC
góc DAI+góc DMI=180 độ
=>DAIM nội tiếp
b: Sửa đề: AI*IC=BI*IM
Xét ΔIAB vuông tại A và ΔIMC vuông tại M có
góc AIB=góc MIC
=>ΔIAB đồng dạng với ΔIMC
=>IA/IM=IB/IC
=>IA*IC=IM*IB
c: góc ADI=90 độ-góc DBC
góc ACB=90 độ-góc DBC
=>góc ADI=góc ACB=1/2*góc AOB

Em kham khảo link này nhé.
Câu hỏi của Trần Đức Thắng - Toán lớp 9 - Học toán với OnlineMath