Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

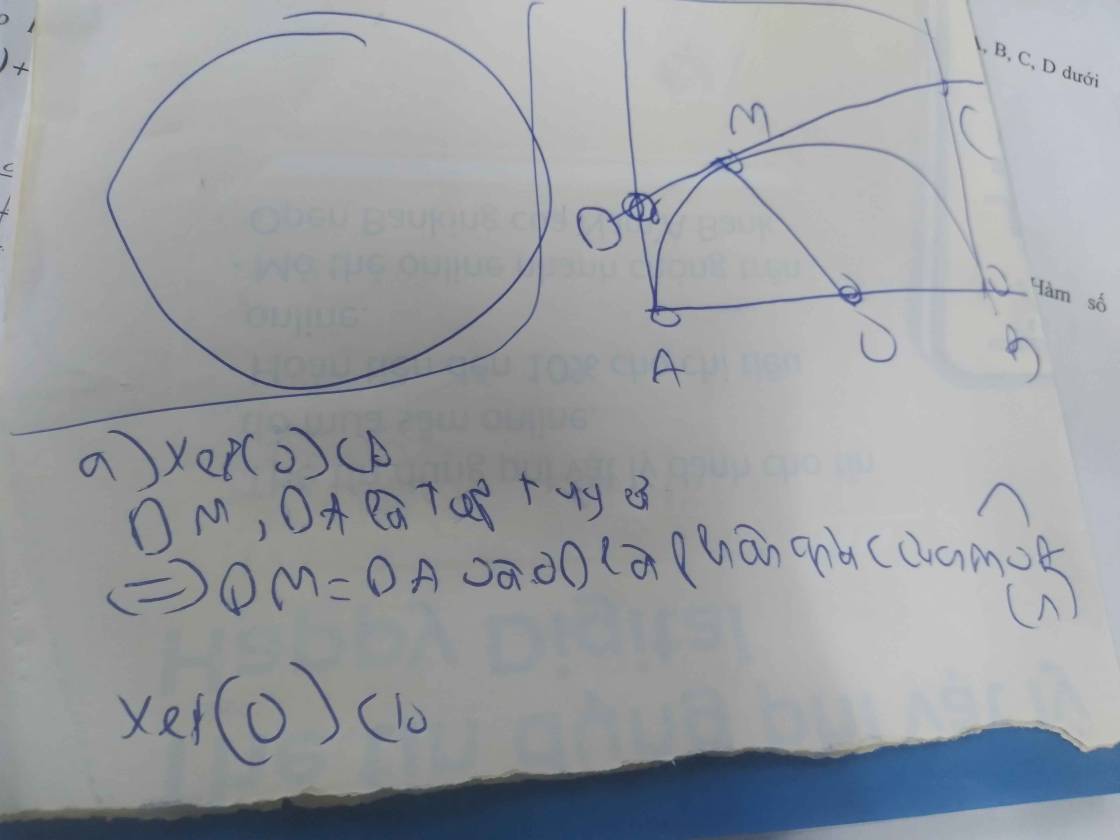
a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: OC là tia phân giác của \(\widehat{AOM}\)
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: OD là tia phân giác của \(\widehat{BOM}\)
Ta có: \(\widehat{AOM}+\widehat{BOM}=180^0\)
\(\Leftrightarrow2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
hay \(\widehat{COD}=90^0\)

a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: MC+MD=CD
mà MC=CA
và MD=DB
nên CD=AC+BD

1: Xét (O) có
CA là tiếp tuyến có A là tiếp điểm
CM là tiếp tuyến có M là tiếp điểm
Do đó: OC là tia phân giác của \(\widehat{MOA}\)
Xét (O) có
DB là tiếp tuyến có B là tiếp điểm
DM là tiếp tuyến có M là tiếp điểm
Do đó: OD là tia phân giác của \(\widehat{MOB}\)
Ta có: \(\widehat{COD}=\widehat{COM}+\widehat{DOM}\)
\(=\left(\widehat{MOA}+\widehat{MOB}\right)\cdot\dfrac{1}{2}\)
\(=180^0\cdot\dfrac{1}{2}=90^0\)
hay ΔCOD vuông tại O
Xét (O) có
CA là tiếp tuyến có A là tiếp điểm
CM là tiếp tuyến có M là tiếp điểm
Do đó: CM=CA
Xét (O) có
DB là tiếp tuyến có B là tiếp điểm
DM là tiếp tuyến có M là tiếp điểm
Do đó: DB=DM
\(AC\cdot BD=CM\cdot MD=OM^2\) không phụ thuộc vào vị trí của M

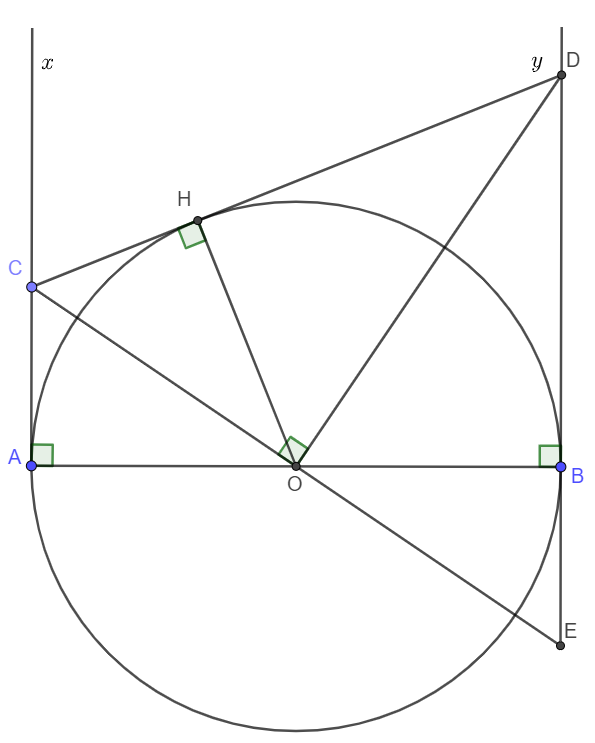
Vẽ OH\perp CD\left(H\in CD\right)OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có \Delta OAC=\Delta OBE\left(g.c.g\right)\Rightarrow OC=OEΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH\perp DC,OB\perp DE\Rightarrow OH=OB.OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH\perp CD,OH=OB=rOH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).
Vẽ OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có ΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).

Gọi H là chân đường vuông góc hạ từ O xuống CD
Ta CM : OH = OB = R ( O )
Tia CO cắt tia đối của tia By tại E
Xét tam giác OAC và OBE có :
góc A + góc B = 900 ( t/c tiếp tuyến )
góc AOC = BOE ( đối đỉnh )
OA = OB (=R)
=> tam giác OAC = OBE ( g.c.g ) => OC = OE
Tam giác DEC có DO vừa là đường cao vừa là trung tuyến nên là tam giác cân. Khi đó DO cũng là đường phân giác
=> Ta có : OH vuông góc CD, OH = OB = R ( O ) nên CD tiếp xúc với (O) tại H