K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

8 tháng 2 2022
\(a,\\ \widehat{CAM}=\widehat{CNM}=90^0\\ \Rightarrow CNMA.là,tứ.giác.nội.tiếp\\ \widehat{MND}=\widehat{MBD}=90^0\\ \Rightarrow NMBF.là.tứ,giác.nội.tiếp\\ b,CNMA.nội.tiếp\\ \Rightarrow\widehat{NAM}=\widehat{NCM}\\ MNDB.nội.tiếp\\ \Rightarrow\widehat{NDM}=\widehat{NBM}\)
\(\Delta CMD.và.\Delta AnpNB:\\ \widehat{NAM}=\widehat{NCM};\widehat{NDM}=\widehat{ABM}\\ \Rightarrow\Delta....đồng.dạng.\Delta....\)
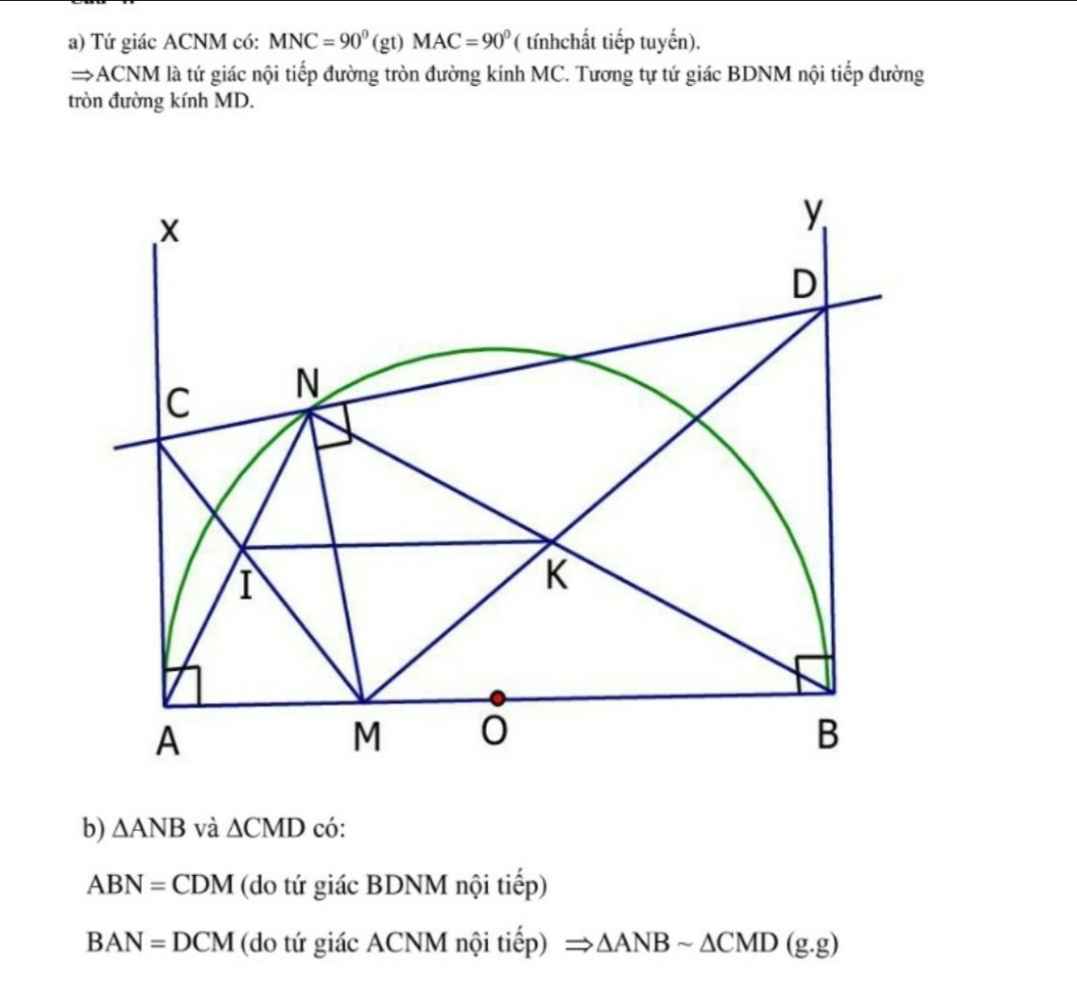
a, xét từ giác AMNC có
\(\widehat{CAM}\)=90∘CAM^=90∘ (Ac là tiếp tuyến của (O) , ˆ
\(\widehat{CNM}\)=90∘CNM^=90∘ (MN vuông góc với CD) => ˆ\(\widehat{CAM}+\widehat{CNM}\)=180
=> AMNC nội tiếp
Xét tứ giác BMND có ˆ\(\widehat{MNB}\)MBD^=90 ( BD là tiếp tuyến của (O) , \(\widehat{CND}\)=90 ( MN vuông góc với CD)
=> \(\widehat{MND}+\widehat{NAC}\)NAC^=180
=> Tứ giác BDMN nội tiếp
b, Ta có \(\widehat{CMN}=\widehat{NAC}\)NAC^ (cùng chắn CN)
=> \(\)\(\widehat{CMN}\)CMN^=1212 cung AN(1)
Ta cũng có\(\widehat{NMD}+\widehat{NMD}\)NBD^ (cùng chắn cung ND)
\(\widehat{NMD}\)=1212 cung NB(2)
Từ (1) và (2) => \(\widehat{CMD}+\widehat{NMD}\)NMD^= 1212 (cung AN + cung NB)
=> \(\widehat{CMD}\)= 1212 cung AB = 18021802=90
=> tam giác CMD vuông tại M
Vì NMBD nội tiếp => \(\widehat{NDM}+\widehat{NBM}\)NBM^ ( góc nội tiếp cùng chắn cung AM)
Mà \(\widehat{MCD}+\widehat{NBM}\)=90
=> \(\widehat{MCD}+\widehat{NBM}\)NBM^=90 (1)
Mặt khác \(\widehat{NAB}+\widehat{NBA}\)NBA^=90 (2)
Từ (1) và (2) => \(\widehat{MCD}=\widehat{NAB}\)
Xét tam giác ANB và CMD ta cs
\(\widehat{ANB}=\widehat{CMD}\) (=90)
\(\widehat{MCD}=\widehat{NAD}\)
=> 2 tam giác này bằng nhau