Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
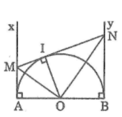
Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
O I 2 = MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra : AM.BN = O I 2 = R 2
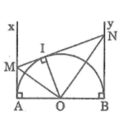
Gọi I là tiếp điểm của tiếp tuyến MN với đường tròn (O). Nối OI
Ta có: 
(hai góc kề bù)
OM là tia phân giác của góc AOI (tính chất hai tiếp tuyến cắt nhau)
ON là tia phân giác của góc BOI (tính chất hai tiếp tuyến cắt nhau)
Suy ra : OM ⊥ ON (tính chất hai góc kề bù)
Vậy 
bạn tự vẽ hình giúp mik nha
a) áp dụng t/c 2 tiếp tuyến cắt nhau ta có
OM là tia phân giác \(\widehat{AOI}\)
ON là tpg \(\widehat{IOB}\)
mà:\(\widehat{AOI}+\widehat{BOI}=180^o\)\(\Rightarrow OM\perp ON\)(t/c 2 góc kề bù)
vậy \(\widehat{MON}=90^o\)
b)từ t/c 2 tiếp tuyến cắt nhau ta có
MA=MI;BN=NI
\(\Rightarrow\)AM+BN=MI+NI=MN9(đpcm)
c)ta có:AM.BN=MI.NI(1)
xét \(\Delta MON\) vuông tại O có
MI.NI(đlý)=\(OI^2=R^2\)(2)
từ (1) và (2)\(\Rightarrow AM.BN=R^2\)
gọi H là điểm tiếp điểm của MN với nữa đường tròn
ta có : OM là tia phân giác của góc AOH (theo tính chất 2 tiếp tuyến cắt nhau)
ON là tia phân giác của góc BOH (theo tính chất 2 tiếp tuyến cắt nhau)
mà 2 góc MOH và HON kề bù \(\Rightarrow\) MON = 900
b) AM = HM và BN = HN (tính chất 2 tiếp tuyến cắt nhau) (1)
nên MN = HM + HN = AM + BN
vậy MN = AM + BN (đpcm)
c) từ (1) ta có : AM.BN = HM.HN
ta lại có : HM HN = OH2 = R2 (hệ thức lượng)
\(\Rightarrow\) AM.BN = R2 (đpcm)
a: Xét (O) có
ME là tiếp tuyến
MA là tiếp tuyến
Do đó: ME=MA và OM là tia phân giác của góc AOE(1)
Xét (O) có
NE là tiếp tuyến
NB là tiếp tuyến
Do đó: NE=NB và ON là tia phân giác của góc BOE(2)
Từ (1) và (2) suy ra \(\widehat{MON}=\dfrac{1}{2}\cdot\left(\widehat{EOA}+\widehat{EOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
b: Ta có: MN=ME+NE
nên MN=MA+NB
c: Xét ΔOMN vuông tại O có OE là đường cao
nên \(OE^2=EM\cdot EN\)
hay \(AM\cdot BN=R^2\)
b: Xét (O) có
MC là tiếp tuyến
MA là tiếp tuyến
Do đó: MC=MA
Xét (O) có
NC là tiếp tuyến
NB là tiếp tuyến
Do đó: NC=NB
Ta có: MN=MC+NC
nên MN=MA+NB
Ta có: MA = MI (tính chất hai tiếp tuyến cắt nhau)
NB = NI (tính chất hai tiếp tuyến cắt nhau)
Mà: MN = MI + IN
Suy ra: MN = AM + BN