Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B D C M
1. Ta có AD // OM // BC ; OA = OB
=> OM là đường trung bình của hình thang ABCD => M là trung điểm CD => MC = MD
2. Vì OM là đường trung bình của hình thang ABCD nên : \(OM=\frac{AD+BC}{2}\Rightarrow AD+BC=2OM\)không đổi.
3. Dễ thấy M là tâm của đường tròn đường kính CD vì MC = MD
Lại có AD vuông góc với MD => đpcm
4. Ta có : \(S_{ABCD}=\frac{1}{2}.\left(AD+BC\right).CD=OM.CD\)
Vì OM không đổi nên S.ABCD lớn nhất <=> CD lớn nhất <=> CD = AB
Vậy max (S.ABCD) = OM . AB = R.(2R) = 2R2 với R = AB/2

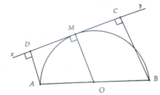
Ta có ABCD là hình thang vuông tại C và D
Mà O Là trung điểm AB và OM vuông góc với CD( tiếp tuyến của (O)
=> AD+BC=2OM=2R. Chú ý rằng CD ≤ AB (hình chiếu đường xiên)
=> S A B C D = 1 2 A D + B C . C D
= R.CD ≤ R.AB = 2 R 2
Do đó S A B C D lớn nhất khi CD=AB hay M là điểm chính giữa nửa đường tròn đường kính AB

a, 700 góc nào bạn ?
b, Vì AB là tiếp tuyến (O) => ^ABO = 900
AO giao BC = K
AB = AC ; OB = OC = R
Vậy OA là đường trung trực đoạn BC
Xét tam giác ABO vuông tại B, đường cao BK
Áp dụng định lí Pytago tam giác ABO vuông tại B
\(AB=\sqrt{AO^2-BO^2}=\sqrt{16-4}=2\sqrt{3}\)cm
Áp dụng hệ thức : \(BK.AO=BO.AB\Rightarrow BK=\frac{BO.AB}{AO}=\frac{4\sqrt{3}}{4}=\sqrt{3}\)cm
Vì AO là đường trung trực => \(BC=2KB=2\sqrt{3}\)cm
Chu vi tam giác ABC là :
\(P_{ABC}=AB+AC+BC=2AB+BC=4\sqrt{3}+2\sqrt{3}=6\sqrt{3}\)cm

a) ABCD là hình thang vuông ( AD//BC)
Mà OM//AD //BC và O là trung điểm AB
theo định lí về đường TB hình thang => M là trung điểm của DC => MD =MC
b) theo a => OM là đường TB của ABCD => OM = (AD+BC)/2 hay AD+BC = 2 OM = 2R = không đổi
c) M là trung điểm CD => (M;CD/2) là đường tròn đường kính CD
C thuộc (M) mà BC _|_ CD tại C => BC là tiếp tuyến của (M)
D thuộc (M) mà AD_|_ CD tại D => AD là tiếp tuyến của (M)
d) do AD+BC =2R
=> S ( ABCD) lớn nhát khi CD lớn nhát => CD =AB = 2R
khi đó M là điểm chính giữa cung AB