Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, HS tự chứng minh
b, Chứng minh được M N ⏜ = C A ⏜ = C B ⏜
=> ĐPCM

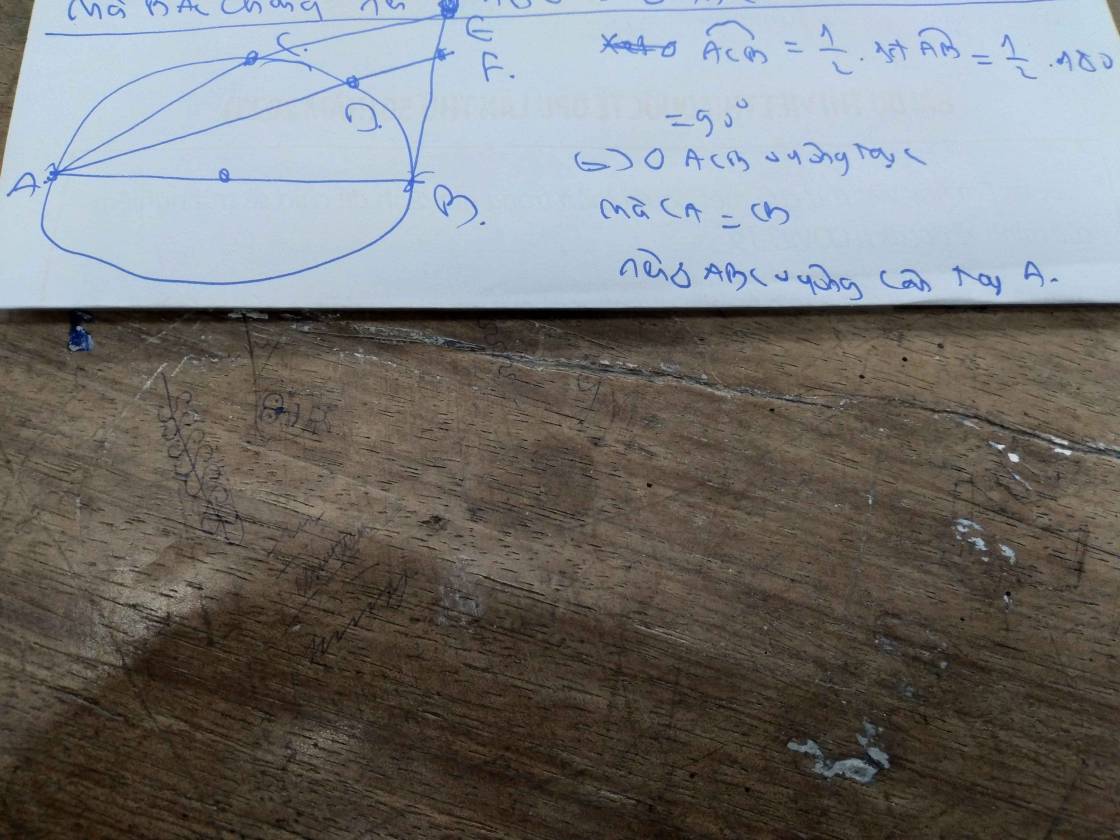
xét đường tròn tâm o có
C là điểm chính giữa nằm trên nửa đường tròn
=> cung CA = cung CB
=> CA=CB điều 1 ...liên hệ giữa cung và dây
mặt khác. góc CBNlaf góc nội tiếp chắn cung CN
góc NMC là góc nội tiếp chắn cung CN
=> góc CBN = góc NMC
lại có cung BN = cung CM
=> BN=MC
xét tam giác CBN và Tam giác NMC có
CN chung
BN = MC
góc CBN= góc NMC
=> 2 tam giác bằng nhau => MN = BC điều 2
từ 1 và 2 => MN= CA =CB

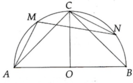
a) Xét (O) có
M là một điểm nằm trên cung \(\stackrel\frown{CA}\)(gt)
nên \(sđ\stackrel\frown{CM}+sđ\stackrel\frown{MA}=sđ\stackrel\frown{CA}\)(1)
Xét (O) có
N là một điểm nằm trên cung \(\stackrel\frown{CB}\)(gt)
nên \(sđ\stackrel\frown{CN}+sđ\stackrel\frown{NB}=sđ\stackrel\frown{CB}\)(2)
Xét (O) có AB là đường kính(gt)
nên O là trung điểm của AB
Xét ΔCAB có
CO là đường cao ứng với cạnh AB(gt)
CO là đường trung tuyến ứng với cạnh AB(O là trung điểm của AB)
Do đó: ΔCAB cân tại C(Định lí tam giác cân)
⇒CA=CB
⇒\(sđ\stackrel\frown{CA}=sđ\stackrel\frown{CB}\)(3)
Từ (1), (2) và (3) suy ra \(sđ\stackrel\frown{CM}+sđ\stackrel\frown{AM}=sđ\stackrel\frown{CN}+sđ\stackrel\frown{NB}\)
mà \(sđ\stackrel\frown{CM}=sđ\stackrel\frown{BN}\)(gt)
nên \(sđ\stackrel\frown{AM}=sđ\stackrel\frown{CN}\)
hay \(\stackrel\frown{AM}=\stackrel\frown{CN}\)(đpcm)
Xét (O) có
AM là dây cung(A,M∈(O))
CN là dây cung(C,N∈(O))
\(\stackrel\frown{AM}=\stackrel\frown{CN}\)(cmt)
Do đó: AM=CN(Liên hệ giữa cung và dây)

b) Do \(\stackrel\frown{AM}=\stackrel\frown{CN}\) (theo câu a) => \(\widehat{AOM}=\widehat{CON}\)
Mà \(\widehat{AOM}+\widehat{MOC}=\widehat{AOC}=90^o\) => \(\widehat{NOC}+\widehat{MOC}=\widehat{MON}=90^o\)
Xét ΔOMN và ΔOAC có: \(\widehat{MON}=\widehat{AOC}=90^o\)
OA = OM (=bán kính nửa đường tròn)
OC = ON (=bán kính nửa đường tròn)
=> ΔOMN = ΔOAC (c.g.c) => MN = AC (2 cạnh tương ứng)
CMTT => ΔOMN = ΔOBC => MN = BC (2 cạnh tương ứng)
=> MN = AC = BC

a: sđ cung AC=2/3*180=120 độ
=>sđ cung AM=sđ cung MC=120/2=60 độ
sđ cung NB=sđ cung NC=60/2=30 độ
góc MIC=1/2(sđ cung AB+sđ cung MC)
=1/2(180+60)=120 độ
b: N là điểm chính giữa của cung BC
=>ON vuông góc bC
=>ON//AC
=>DN vuông góc NO
=>DN là tiếp tuyến của (O)