Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

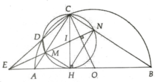
a, Tứ giác CMHN là hình chữ nhật
b, Ta có
O
C
A
^
=
O
A
C
^
C B A ^ = A C H ^ ; A C H ^ = C M N ^
=> O C A ^ + C M N ^ = 90 0
Vậy OC ⊥ MN
c, Ta có ∆IOC có E là trực tâm suy ra IN đi qua M và E (đpcm)
d, Ta có E M A ^ = C M N ^ ; C M N ^ = C B A ^ => ∆EMA:∆ENB
Tương tự ∆EMH:∆EHN => EM.EN = E H 2 ngoài ra , ∆EHC vuông tại H có HD là đường cao
=> E H 2 = ED.EC. Từ đó ta có đpcm

1: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp
=>A,E,H,F cùng thuộc một đường tròn
2: Kẻ tiếp tuyến Ax tại A của (O)
Xét (O) có
\(\widehat{xAB}\) là góc tạo bởi tiếp tuyến Ax và dây cung AB
nên \(\widehat{xAB}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BA}\)
Xét (O) có
\(\widehat{ACB}\) là góc nội tiếp chắn cung BA
Do đó: \(\widehat{ACB}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BA}\)
=>\(\widehat{xAB}=\widehat{ACB}\left(1\right)\)
Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>\(\widehat{AEF}=\widehat{AHF}\)
mà \(\widehat{AHF}=\widehat{ACB}\left(=90^0-\widehat{HAC}\right)\)
nên \(\widehat{AEF}=\widehat{ACB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{xAB}=\widehat{AEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ax//EF
Ta có: Ax//EF
OA\(\perp\)Ax
Do đó: OA\(\perp\)EF

Câu 1 là vuông góc với AB chứ không phải vuông góc với A nha. Mình đánh nhanh nên nhầm