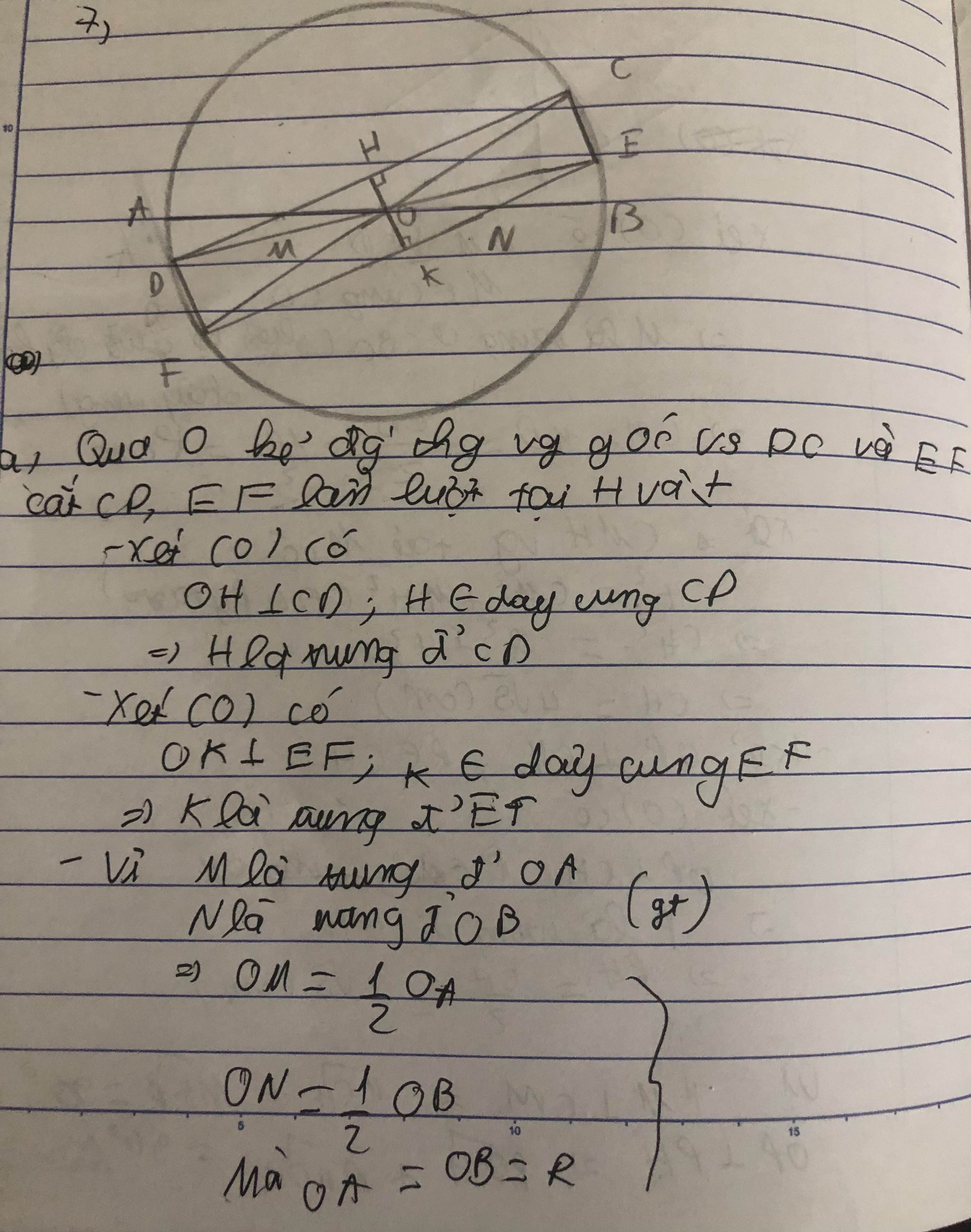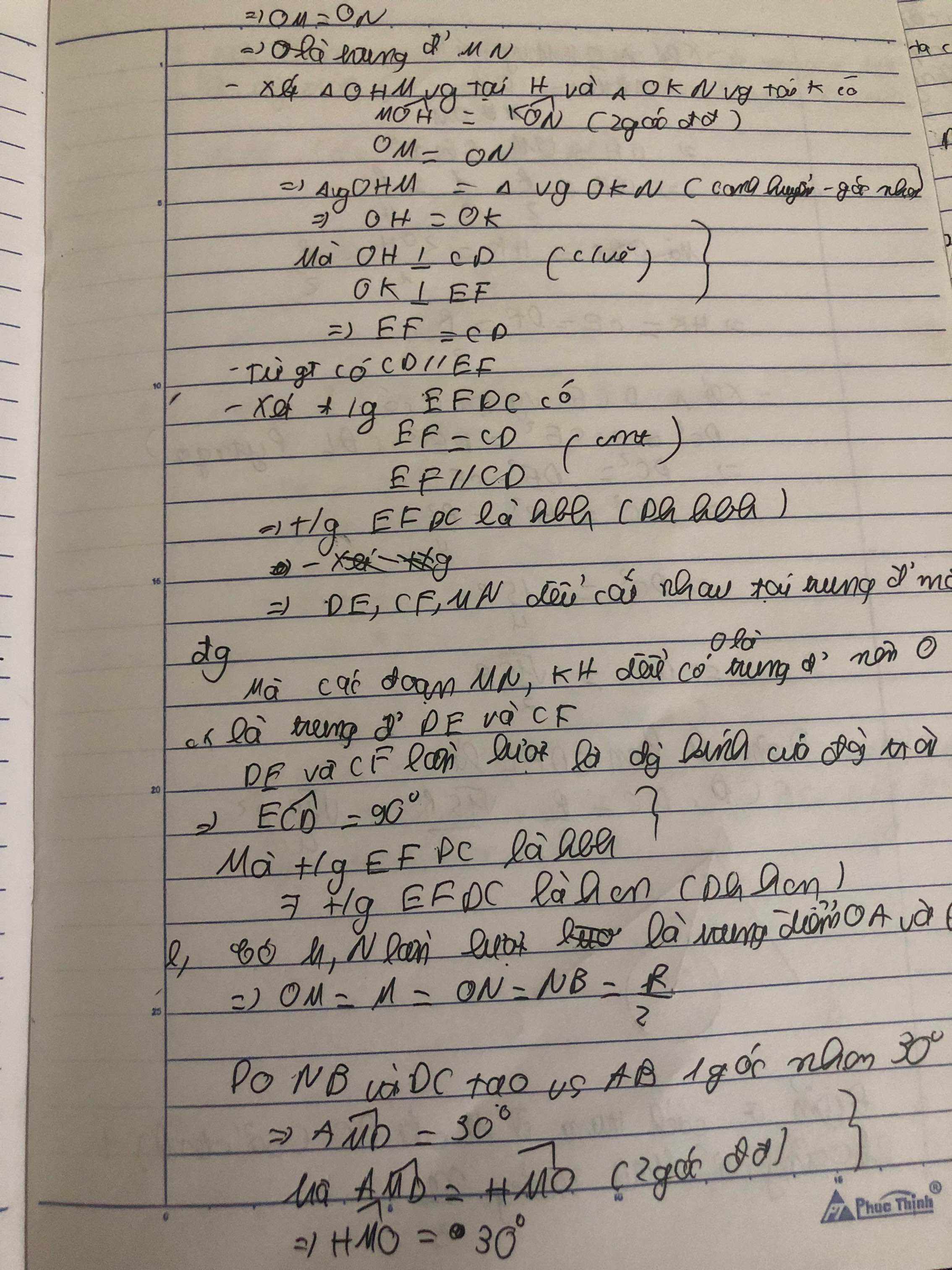Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét hình thang AHKB có
O là trung điểm của AB
OM//AHKB
Do đó: M là trung điểm của HK
b: Kẻ MN vuông góc với AB
Xét tứ giác AHMN có \(\widehat{AHM}+\widehat{ANM}=180^0\)
=>AHMN là tứ giác nội tiếp
=>\(\widehat{MAN}=\widehat{MHN}\)
Xét tứ giác MNBK có \(\widehat{MNB}+\widehat{MKB}=180^0\)
=>MNBK nội tiếp
=>\(\widehat{MBN}=\widehat{MKN}\)
Xét (O) có
ΔMAB nội tiếp
AB là đường kính
Do đó: ΔMAB vuông tại M
=>\(\widehat{MAB}+\widehat{MBA}=90^0\)
=>\(\widehat{NHK}+\widehat{NKH}=90^0\)
=>ΔNKH vuông tại N
ΔNKH vuông tại N có NM là trung tuyến
nên MH=MN
Xét (M) có
MN là bán kính
AB vuông góc MN tại N
Do đó: AB là tiếp tuyến của (M)
=>ĐPCM

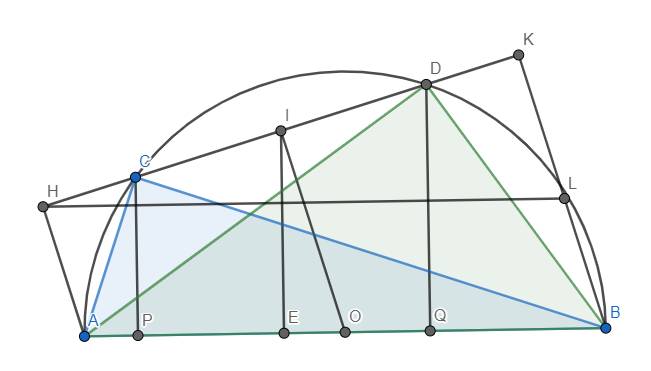
a) Ta thấy OI//AH//BK \(\left(\perp CD\right)\).
Xét hình thang ABKH (AH//BK), O là trung điểm AB. OI//AH \(\left(I\in HK\right)\) nên I là trung điểm HK.
b) Hạ \(CP\perp AB\) tại P, \(DQ\perp AB\) tại Q. Khi đó IE//CP//DQ \(\left(\perp AB\right)\).
Xét hình thang CDQP (CP//DQ) có I là trung điểm CD (hiển nhiên), IE//CP và \(E\in PQ\) nên IE là đường trung bình của hình thang CDQP \(\Rightarrow IE=\dfrac{CP+DQ}{2}\)
Lại có \(S_{ACB}=\dfrac{1}{2}AB.CP\), \(S_{ADB}=\dfrac{1}{2}.AB.DQ\)
\(\Rightarrow S_{ACB}+S_{ADB}=AB.\dfrac{CP+DQ}{2}=AB.IE\) (đpcm)
c) Ta có \(S_{AHKB}=\dfrac{AH+BK}{2}.HK=OI.HK\)
Do dây CD có độ dài không đổi nên khoảng cách từ O đến dây CD là OI cũng không đổi. Như vậy ta chỉ cần tìm vị trí của C để HK lớn nhất.
Thật vậy, dựng hình bình hành ABLH. Khi đó vì BK//AH nên \(L\in BK\). Đồng thời ta luôn có \(HK\le HL=AB\), suy ra \(S_{AHKB}\le OI.AB\).
Dấu "=" xảy ra \(\Leftrightarrow HK=HL\) \(\Leftrightarrow K\equiv L\) \(\Leftrightarrow\) AHKB là hình bình hành \(\Leftrightarrow\) HK//AB hay CD//AB \(\Rightarrow OI\perp AB\). Vậy C là điểm sao cho \(OI\perp AB\).
(Nếu muốn tìm cụ thể vị trí của C, thì mình nói luôn nó là điểm C sao cho \(sđ\stackrel\frown{AC}=180^o-2arc\cos\left(\dfrac{CD}{AB}\right)\) nhé. Chứng minh cái này dễ, mình nhường lại cho bạn.)
Chỗ vị trí C mình sửa lại là \(sđ\stackrel\frown{AC}=90^o-arc\sin\dfrac{CD}{AB}\) nhé.