Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
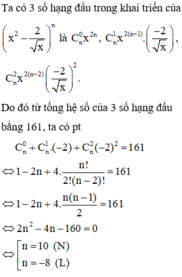
Vậy n = 10.
Ta có số hạng tổng quát trong khai triển trên là
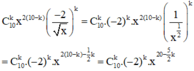
Vì a là hệ số của số hạng không chứa x trong khai triển nên ta cho
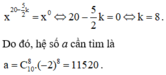

Xét 3 2 k + 1 C 2 n 2 k = 3 2 k + 1 C 2 n + 1 2 k + 1 và - 1 2 k + 1 C 2 n 2 k = - 1 2 k + 1 C 2 n + 1 2 k + 1
Điều kiện bài toán tương đương với:
3 2 n + 1 C 2 k 2 n + C 2 n + 1 3 - 1 2 n + 1 C 2 n + 1 2 + C 2 n + 1 4 = 10923 5 ⇔ 2 2 n + 1 . 2 2 n + 1 2 - 1 2 n + 1 2 2 n + 1 2 - C 2 n + 1 0 = 10923 5
Giải phương trình này hết sức đơn giản ta tìm được n = 7. Ta có:
a b 3 + b 2 b 2 3 a a 2 3 21 ∑ k = 0 21 C 21 k a k 3 b k 3 b 8 ( 21 - k ) 3 a - 5 21 - k 3
Hệ số của số hạng có tỉ số lũy thừa của a và b bằng - 1 2 nên
k 3 - 35 + 5 k 35 - k 3 + 56 - 8 k 3 = - 1 2 ⇒ k = 14
Vậy hệ số của bài toán thỏa mãn yêu cầu bài toán là C 21 14 = 116280
Đáp án D

Đáp án C
* log 1 16 x xác định khi x > 0
* log 16 log 1 16 x xác định khi log 1 16 x > 0 = log 1 16 1 ⇔ 0 < x < 1
* log 1 4 log 16 log 1 16 x xác định khi
log 16 log 1 16 x > 0 = log 16 1 ⇒ log 1 16 x > 1 = log 1 16 1 16 ⇒ x < 1 16
* log 4 log 1 4 log 16 log 1 16 x xác định khi
log 1 4 log 16 log 1 16 x > 0 = log 1 4 1 ⇒ log 16 log 1 16 x < 1 = log 16 16
⇒ log 1 16 x < 16 = log 1 16 1 16 16 ⇒ x > 1 16 16
* log 1 2 log 4 log 1 4 log 16 log 1 16 x xác định khi
log 4 log 1 4 log 16 log 1 16 x > 0 = log 4 1
⇒ log 1 4 log 16 log 1 16 x > 1 = log 1 4 1 4 ⇒ log 16 log 1 16 x < 1 4 = log 16 2
⇒ log 1 16 x < 2 = log 1 16 1 16 2 ⇒ x > 1 16 2
Kết hợp tất cả các điều kiện ta được
1 16 2 < x < 1 16 ⇒ D = 1 16 2 ; 1 16 ⇒ b − a = 15 256 ⇒ m + n = 271