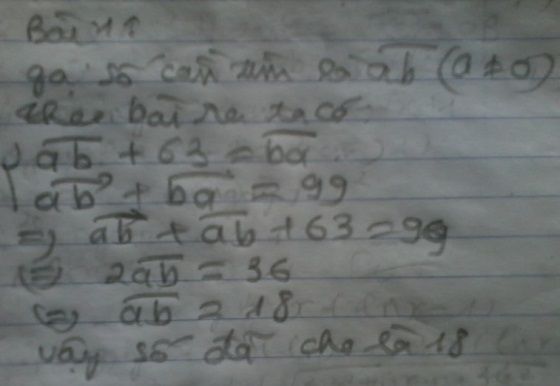Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi số đã cho là \(\overline{xy}\left(x\inℕ^∗,1\le x\le9,y\inℕ,0\le y\le9\right)\)
Ta có: \(\overline{xy}=10x+y\)
Theo bài ra, đổi chỗ 2 chữ số đã cho thì được số mới nhỏ hơn số cũ là 18, ta có phương trình: \(10x+y=10y+x+18\)
Lại có, tổng số mới và số cũ là 176, ta có phương trình: \(10x+y+10y+x=176\)
Ta có hệ phương trình:
\(\hept{\begin{cases}10x+y=10y+x+18\\10x+y+10y+x=176\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}9x-9y=18\\11x+11y=176\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y=2\\x+y=16\end{cases}}\)
\(\hept{\begin{cases}x=9\\y=7\end{cases}}\)
Vậy số cần tìm là 97.
Gọi số cần tìm là a b ¯ , a ∈ ℕ * , b ∈ ℕ * ; a , b ≤ 9
Đổi chỗ hai chữ số của nó thì ta được một số mới là b a ¯
Ta có hệ phương trình:
b a ¯ − a b ¯ = 63 b a ¯ + a b ¯ = 99 ⇔ 2 a b ¯ = 36 b a ¯ + a b ¯ = 99 ⇔ a b ¯ = 18 b a ¯ = 81 (thỏa mãn)
Vậy số cần tìm là 24 nên tổng các chữ số là 2 + 4 =6
Đáp án: D
Gọi chữ số hàng chục là x, chữ số hàng đơn vị là y.
Điều kiện x ∈N* và x ≤ 9; y ∈N* và y ≤ 9.
Số có hai chữ số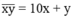 
và số đổi chỗ:
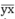= 10y + x
Đổi chỗ hai chữ số thì được một số lớn hơn số đã cho là 63, ta có:
(10y + x) – (10x + y) = 63
Tổng của số đã cho và số mới tạo thành bằng 99, ta có:
(10x + y) + (10y + x) = 99
Ta có hệ phương trình:
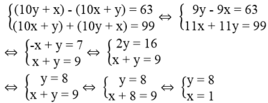
Ta thấy x = 1, y = 8 thỏa điều kiện bài toán.
Vậy số cần tìm là 18.
Gọi số cần tìm là a b ¯ , a ∈ ℕ * , b ∈ ℕ * ; a , b ≤ 9
Đổi chỗ hai chữ số của nó thì ta được một số mới là b a ¯
Ta có hệ phương trình:
b a ¯ − a b ¯ = 63 b a ¯ + a b ¯ = 99 ⇔ 2 a b ¯ = 36 b a ¯ + a b ¯ = 99 ⇔ a b ¯ = 18 b a ¯ = 81 (thỏa mãn)
Vậy số cần tìm là 18 nên tổng các chữ số là 1 + 8 = 9
Đáp án: A