K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

26 tháng 8 2021
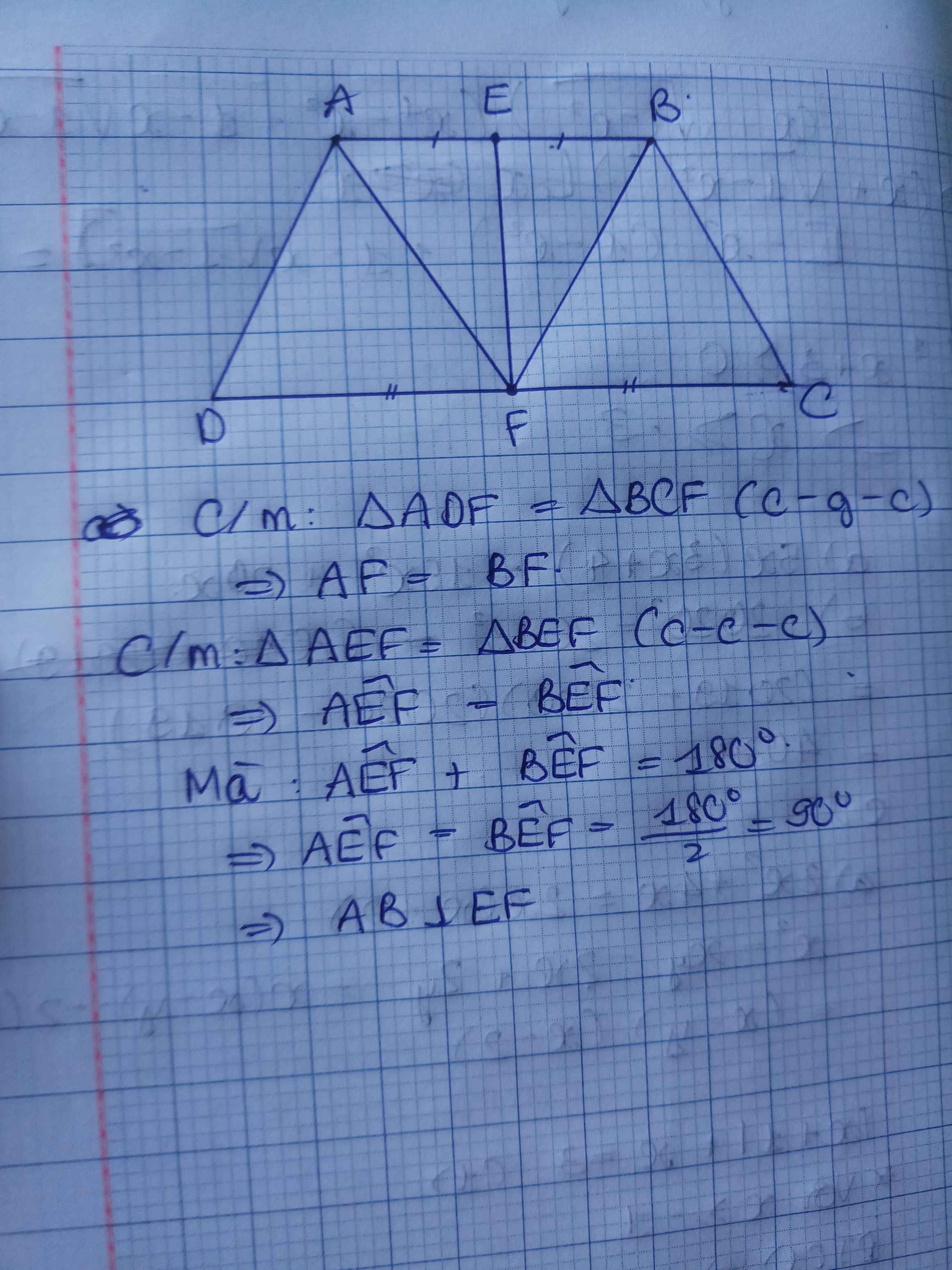
Xét ΔADF và ΔBCF có
AD=BC
\(\widehat{D}=\widehat{C}\)
FD=FC
Do đó: ΔADF=ΔBCF
Suy ra: FA=FB
Xét ΔFAB có FA=FB
nên ΔFAB cân tại F
mà FE là đường trung tuyến ứng với cạnh đáy AB
nên FE là đường cao ứng với cạnh AB
hay FE\(\perp\)AB

CM
29 tháng 3 2019
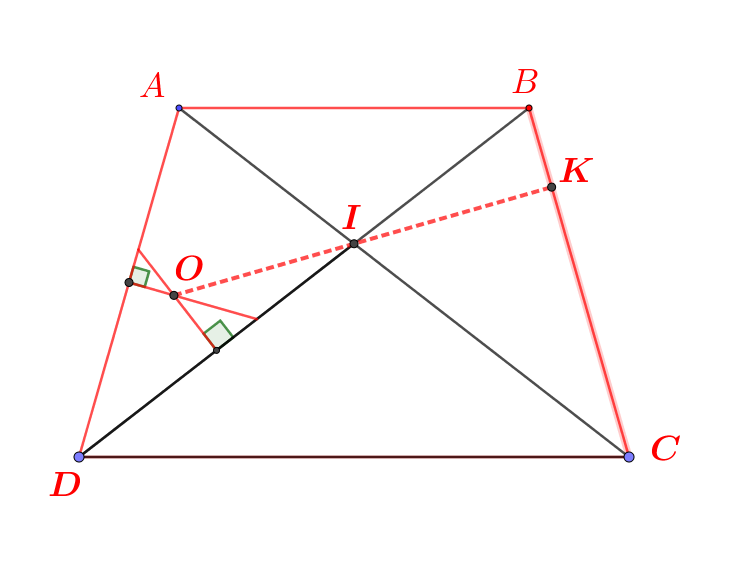
Gọi O là giao điểm của AC và BD.
Chứng minh: OE ^ AB.
Tương tự, có OF ^ CD.
Suy ra OF ^ AB. Vậy EF ^ AB

GH
22 tháng 6 2023
2)
Có: \(\left\{{}\begin{matrix}AB=AD\left(gt\right)\\AD=BC\left(2.cạnh.bên.hình.thang.cân\right)\end{matrix}\right.\)
\(\Rightarrow AB=BC\Rightarrow\Delta ABC.cân.tại.B\)
Mà AB // ED (gt)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\left(so.le.trong\right)\)
\(\Rightarrow\widehat{ACB}=\widehat{ACD}\)
=> CA là tia phân giác của góc C.