Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bạn xem lời giải của mình nhé:
Giải:
Tổng của 5 số đó là:
138 x 5 = 690
Tổng của 3 số đầu tiên là:
127 x 3 = 381
Tổng của 3 số cuối cùng là:
148 x 3 = 444
Tổng của 2 số đàu tiên là:
690 - 444 = 246
Số ở giữa là số thứ 3, nên số ở giữa là:
381 - 246 = 135
Đáp số: 135
Chúc bạn học tốt!
Mk làm thế này có đúng ko
138 là trung bình cộng của 5 số, nên tổng 5 số là :
138 x 5 = 690.
Tổng của ba số đầu tiên là :
127 x 3 =381.
Tổng của ba số cuối cùng là :
148 x 3 = 444.
Tổng của hai số đầu tiên là :
690 - 444 = 246.
Số ở giữa là số đứng thứ ba, nên số đó là :
381 - 246 = 135.
Đáp số: 135
138 là trung bình cộng của 5 số, nên tổng 5 số là :
138 x 5 = 690.
Tổng của ba số đầu tiên là :
127 x 3 =381.
Tổng của ba số cuối cùng là :
148 x 3 = 444.
Tổng của hai số đầu tiên là :
690 - 444 = 246.
Số ở giữa là số đứng thứ ba, nên số đó là :
381 - 246 = 135.
Đáp số: 135
Chọn C.
Vì số học sinh là số chẵn nên số trung vị của 100 số liệu này là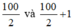 
hay 50 và 51.
Vậy số trung vị của 100 số liệu là chiều cao trung bình của học sinh thứ 50 và 51.
Chọn A.
Do 99 là số lẻ nên số trung vị của dãy số liệu trên là số đứng ở vị trí chính giữa ; tức là giá trị đứng ở vị trí thứ 50.
Mẫu số liệu trên được xếp có 11 số liệu nên \({M_e} = 6\).
Ví dụ, ta có bảng đo chiều cao của các bạn trong tổ như sau:
160 | 162 | 164 | 165 | 172 | 174 | 177 | 178 | 180 |
a) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
160 162 164 165 172 174 177 178 180
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{160\;\; + 162\;\; + 164\;\;\; + \;\;165\;\; + \;172\;\; + \;174\;\; + \;177\; + \;\;178\; + \;180}}{9} = \frac{{1532}}{9}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 9 số liệu ( lẻ ) nên trung vị \({Q_2} = 172\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 160 162 164 165 là: \({Q_1} = 163\)
- Trung vị của dãy 174 177 178 180 là: \({Q_3} = 177,5\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 163\), \({Q_2} = 172\), \({Q_3} = 177,5\)
b) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 180 - 160 = 20\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 177,5 - 163 = 14,5\)
c) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {160 - \overline x } \right)}^2} + {{\left( {162 - \overline x } \right)}^2} + ... + {{\left( {180 - \overline x } \right)}^2}} \right]}}{9} \approx 50,84\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 7,13\)
a) Trong mẫu số liệu (1), hiệu giữa số đo lớn nhất và số đo nhỏ nhất là
\(R = {x_{\max }} - {x_{\min }} = 16 - 14 = 2\)
b) +) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần, ta được:
2 5 6 7 8 9 10 11 12 14 16
+) Vậy \({Q_1}{\rm{ }} = 6;{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}9;{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}12\) . Suy ra \({Q_3} - {Q_1}{\rm{ = }}12{\rm{ }} - 6 = 6\)
Số mật khẩu có thể lập được là:
\(2\cdot9\cdot C^4_{10}=3780\left(cái\right)\)
Chọn D.
+ Khi ta đổi chỗ 2 giá trị đứng đầu tiên và cuối cùng cho nhau thì tần số của mỗi giá trị không đổi nên giá trị có tần số lớn nhất không đổi. Do đó; mốt không đổi.
+ Sau khi sắp xếp lại các số liệu (cụ thể là đổ chỗ số đầu tiên và cuối cùng cho nhau) thì ta vẫn được dãy số liệu như ban đầu nên số trung vị không đổi.
+ Tương tự; phương sai không đổi.