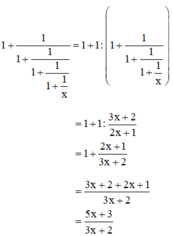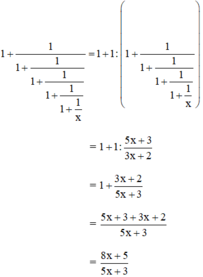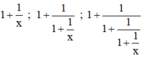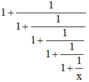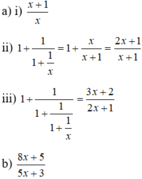K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

AL
26 tháng 5 2016
Mình đã có cách giải, mong các bạn kiểm chứng giúp!
Bất biến ở đây là dù có thay đổi số đã cho như thế nào thì số lúc sau luôn là bội của 7. Thật vậy, giả sử 7^1998 = (A49) ̅ thì A x 100 + 49 chia hết cho 7. Do đó A là bội của 7. Lại có
(A4) ̅ + 45 = ((A + 4)9) ̅ = A x 10 + 49
Là bội của 7. Gọi (Bb) ̅ = A x 10 + 49. Vì thế (Bb) ̅ là bội của 7 và ta cần chứng minh rằng B + 5b là bội của 7. Theo như ta lập luận (Bb) ̅ là bội của 7 suy ra B x 10 + b là bội của 7 và vì thế
B x 20 + 2b là bội của 7
B + 5b
Cộng hai đẳng thức trên ta được B x 21 + 7b là bội của 7. Do đó B + 5b chia hết cho 7, điều phải chứng minh. Kết luận, sau cùng không thể tồn tại số 〖1998〗^7 trên bảng.

CM
21 tháng 1 2017
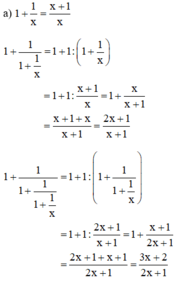
b) + Dự đoán :
Quy luật : Giả sử viết các phân thức trên thành một dãy thì phân thức sau có tử bằng tổng của tử và mẫu của phân thức đứng liền trước và mẫu bằng tử của phân thức đứng liền trước đó.
Do đó :
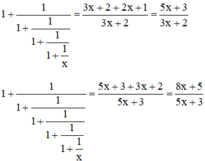
+ Kiểm chứng :