NB
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
1
22 tháng 9 2021
a: Ta có: \(A=\sqrt{4-\sqrt{15}}\cdot\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\)
\(=\sqrt{8-2\sqrt{15}}\cdot\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\)
\(=\left(8-2\sqrt{15}\right)\left(4+\sqrt{15}\right)\)
\(=32+8\sqrt{15}-8\sqrt{15}-30\)
\(=2>\sqrt{3}\)
DT
0
19 tháng 7 2021
Bài 2:
a) Để hàm số đồng biến thì m+1>0
hay m>-1
b) Để hàm số đi qua điểm A(2;4) thì
Thay x=2 và y=4 vào hàm số, ta được:
\(\left(m+1\right)\cdot2=4\)
\(\Leftrightarrow m+1=2\)
hay m=1
c) Để hàm số đi qua điểm B(2;-4) thì
Thay x=2 và y=-4 vào hàm số, ta được:
\(2\left(m+1\right)=-4\)
\(\Leftrightarrow m+1=-2\)
hay m=-3
19 tháng 7 2021
Bài 1:
b) Ta có: \(5\cdot\sqrt{25a^2}-25a\)
\(=5\cdot5\cdot\left|a\right|-25a\)
\(=-25a-25a=-50a\)
7 tháng 7 2021
a)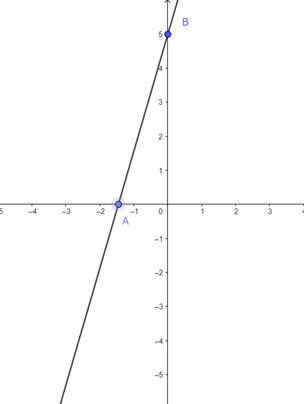 
b) \(tanOAB=\dfrac{OB}{OA}=\dfrac{5}{\dfrac{5}{3}}=3\Rightarrow\widehat{OAB}=71^o34'\)
21 tháng 7 2021
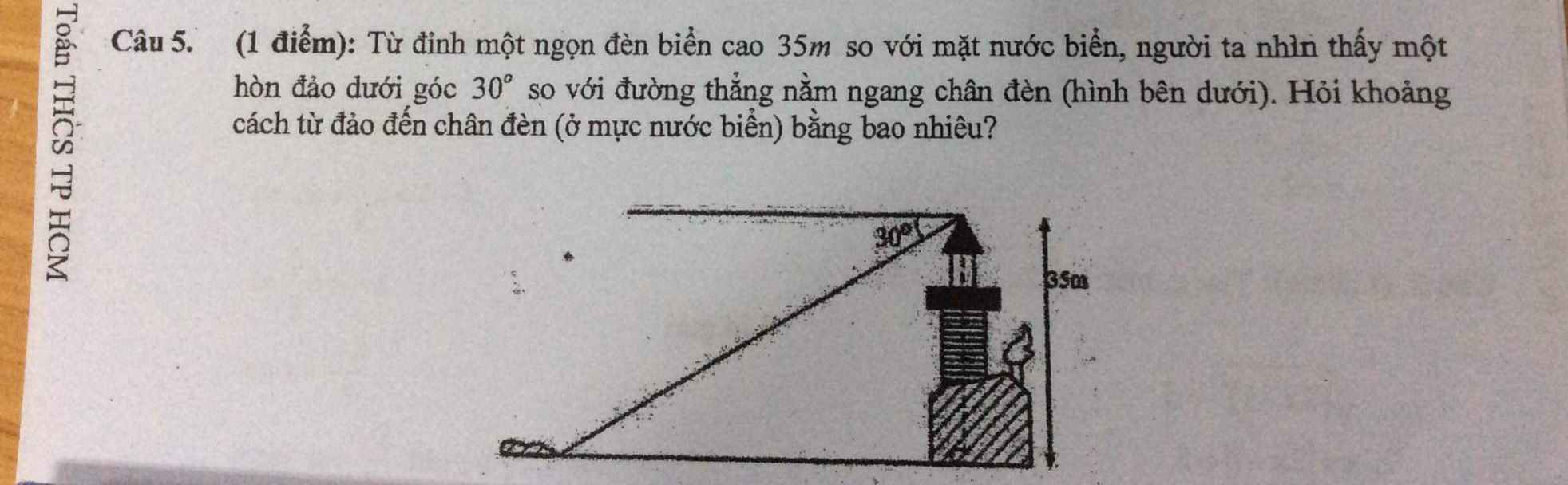
Ta coi hình vẽ là tam giác ABC vuông tại A với B là đỉnh ngọn đèn
góc BCA=30o(2 góc so le trong)
Theo tỉ số lượng giác trong tam giác vuông ta có:
CA=AB : tanC30
CA=35:tan30=60,6(m)
Vậy khoảng cách từ chân đèn đến hòn đảo là 60,6m
23 tháng 7 2021
b) Đặt (d3): y=ax+b
Vì (d3)//(d1) nên \(a=-\dfrac{2}{3}\)
Vậy: (d3): \(y=\dfrac{-2}{3}x+b\)
Thay x=6 vào (d2), ta được:
\(y=-2\cdot6+4=-12+4=-8\)
Thay x=6 và y=-8 vào (d3), ta được:
\(\dfrac{-2}{3}\cdot6+b=-8\)
\(\Leftrightarrow b=-4\)
Vậy: (d3): \(y=\dfrac{-2}{3}x-4\)
23 tháng 7 2021
a) Ta có: \(\sqrt{12+2\sqrt{35}}-\sqrt{12-2\sqrt{35}}\)
\(=\sqrt{7}+\sqrt{5}-\sqrt{7}+\sqrt{5}\)
\(=2\sqrt{5}\)
b) Ta có: \(\left(\dfrac{5+\sqrt{5}}{\sqrt{5}+1}+2\right)\left(\dfrac{5-\sqrt{5}}{\sqrt{5}-1}-2\right)\)
\(=\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)\)
=1
c) Ta có: \(\dfrac{7\sqrt{2}+2\sqrt{7}}{\sqrt{14}}-\dfrac{5}{\sqrt{7}+\sqrt{2}}\)
\(=\sqrt{7}+\sqrt{2}-\sqrt{7}+\sqrt{2}\)
\(=2\sqrt{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 7 2021
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}=7\)
\(\Leftrightarrow\left|x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=7\\x-2=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-5\end{matrix}\right.\)
23 tháng 7 2021
Ta có: \(\sqrt{x^2-4x+4}-5=2\)
\(\Leftrightarrow\left|x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=7\\x-2=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-5\end{matrix}\right.\)
NG
0
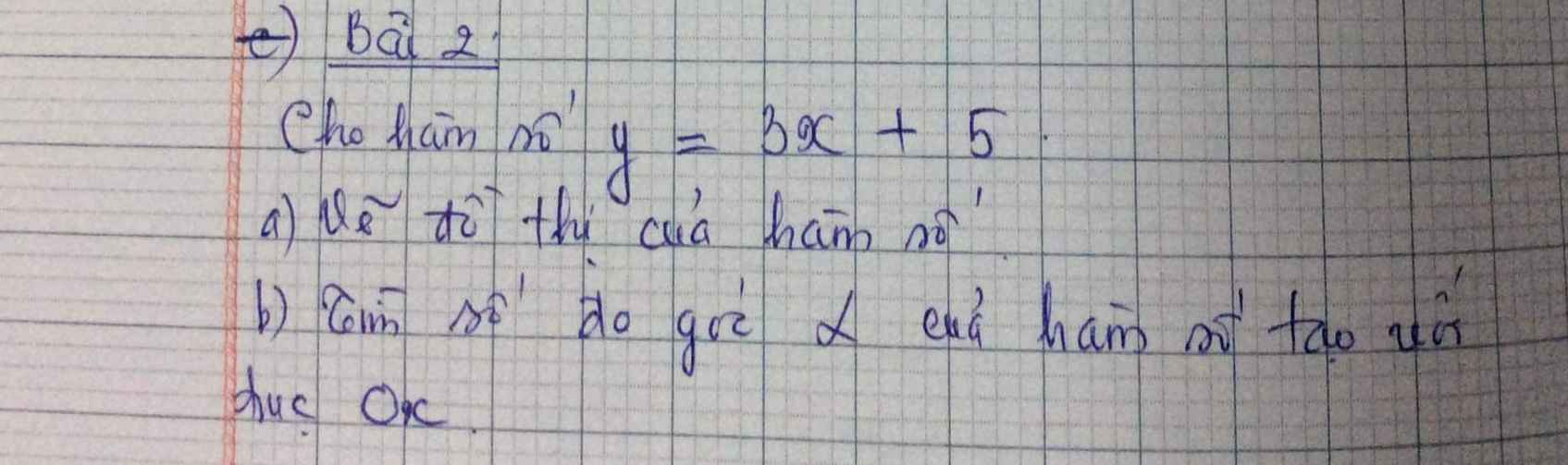
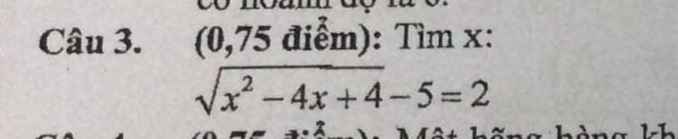
\(A=\sqrt{4-\sqrt{15}}\left(4+\sqrt{15}\right)\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)\\ A=\sqrt{8-2\sqrt{15}}\left(\sqrt{5}-\sqrt{3}\right)\left(4+\sqrt{15}\right)\\ A=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\left(\sqrt{5}-\sqrt{3}\right)\left(4+\sqrt{15}\right)\\ A=\left(\sqrt{5}-\sqrt{3}\right)^2\left(4+\sqrt{15}\right)\\ A=\left(8-2\sqrt{15}\right)\left(4+\sqrt{15}\right)\\ A=2\left(4-\sqrt{15}\right)\left(4+\sqrt{15}\right)=2\left[4^2-\left(\sqrt{15}\right)^2\right]=2\cdot1=2\)
\(A=\sqrt{4-\sqrt{15}}\cdot\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\)
\(=\left(8-2\sqrt{15}\right)\left(4+\sqrt{15}\right)\)
\(=2>\sqrt{3}\)