K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PU
29 tháng 9 2020
Cho mình sửa lại là IA=8cm chứ không phải 80cm nha :v mình nhầm
LB
0
AH
Akai Haruma
Giáo viên
19 tháng 8 2023
Lời giải:
ĐK: $x>0; x\neq 1$
a.
\(P=\frac{3}{\sqrt{x}}+\left[\frac{x}{\sqrt{x}(\sqrt{x}-1)}+\frac{x+1}{\sqrt{x}}-\frac{1}{\sqrt{x}-1}\right].\frac{\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\frac{3}{\sqrt{x}}+\left[\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{1}{\sqrt{x}-1}+\frac{x+1}{\sqrt{x}}\right].\frac{\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\frac{3}{\sqrt{x}}+\left[\frac{\sqrt{x}-1}{\sqrt{x}-1}+\frac{x+1}{\sqrt{x}}\right].\frac{\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\frac{3}{\sqrt{x}}+(1+\frac{x+1}{\sqrt{x}}).\frac{\sqrt{x}}{x+\sqrt{x}+1}=\frac{3}{\sqrt{x}}+\frac{x+\sqrt{x}+1}{\sqrt{x}}.\frac{\sqrt{x}}{x+\sqrt{x}+1}=\frac{3}{\sqrt{x}}+1\)
b.
$P\geq 10\Leftrightarrow \frac{3}{\sqrt{x}}+1\geq 10$
$\Leftrightarrow \frac{3}{\sqrt{x}}\geq 9$
$\Leftrightarrow \sqrt{x}\leq \frac{1}{3}$
$\Leftrightarrow x\leq \frac{1}{9}$
Kết hợp với ĐKXĐ suy ra $0< x\leq \frac{1}{9}$
c.
Để $P$ nguyên thì $\frac{3}{\sqrt{x}}$ nguyên.
Với $x$ nguyên, điều này xảy ra khi $\sqrt{x}$ là ước của $3$
$\Leftrightarrow \sqrt{x}\in\left\{1; 3\right\}$
$\Leftrightarrow x\in\left\{1; 9\right\}$
Vì $x\neq 1$ nên $x=9$
HK
1
4 tháng 2 2022
e: \(=\left|3-\sqrt{2}\right|=3-\sqrt{2}\)
h: \(=3-\sqrt{2}+3+\sqrt{2}=6\)
g: \(=\left|0.1-\sqrt{0.1}\right|=0.1-\sqrt{0.1}\)
i: \(=\left|2\sqrt{2}-3\right|=3-2\sqrt{2}\)
c: \(=\left|2+5\right|=7\)
o: \(=5-2\sqrt{6}-5-2\sqrt{6}=-4\sqrt{6}\)
n: \(=4-2\sqrt{3}+4+2\sqrt{3}=8\)
m: \(=7+2\sqrt{10}-7-2\sqrt{10}=0\)
DD
Đoàn Đức Hà
Giáo viên
28 tháng 5 2022
Câu 10:
Gọi \(H\) là giao điểm của \(MO\) và \(AB\).
Xét tam giác \(MAO\) vuông tại \(A\) đường cao \(AH\):
\(\dfrac{1}{AH^2}=\dfrac{1}{MA^2}+\dfrac{1}{AO^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{R\sqrt{2}}{2}\right)^2}=\dfrac{1}{MA^2}+\dfrac{1}{R^2}\Leftrightarrow MA=R\).
\(S_{MAOB}=S_{MAO}+S_{MBO}\)
\(=\dfrac{1}{2}.AO.MA+\dfrac{1}{2}.OB.MB\)
\(=\dfrac{1}{2}.R.R+\dfrac{1}{2}.R.R=R^2\)
Chọn C.
29 tháng 5 2022
Đài ơi, giải giúp cho Sarah đi, tớ không có viết và giờ vào giường rồi , good nigh
TA
1
7 tháng 7 2023
2:
a: AC=căn 5^2-3^2=4cm
sin B=AC/BC=4/5
cos B=AB/BC=3/5
tan B=4/5:3/5=4/3
cot B=1:4/3=3/4
b: AB=căn 13^2-12^2=5cm
sin B=AC/BC=12/13
cos B=AB/BC=5/13
tan B=12/13:5/13=12/5
cot C=1:12/5=5/12
c: BC=căn 4^2+3^2=5cm
sin B=AC/BC=4/5
cos B=AB/BC=3/5
tan B=4/5:3/5=4/3
cot B=1:4/3=3/4
TA
1
Y
2 tháng 7 2023
\(\sqrt{x^2-4}-x+2=0\\ \Leftrightarrow\sqrt{x^2-4}=x-2\\ \Leftrightarrow\left(\sqrt{x^2-4}\right)^2=\left(x-2\right)^2\)
\(\Leftrightarrow x^2-4-\left(x-2\right)^2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)^2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2-x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)4=0\)
\(\Leftrightarrow x=2\)
Vậy \(S=\left\{2\right\}\)
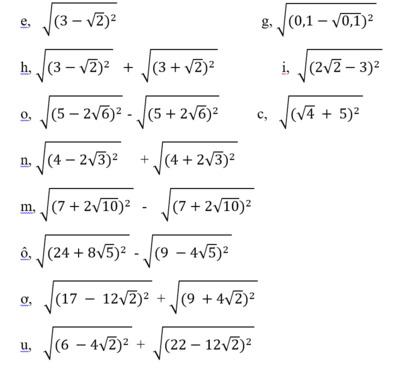
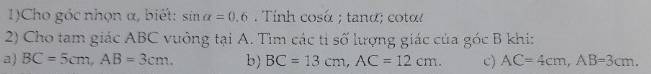
Bài 3:
Gọi giá niêm yết của hai mặt hàng lần lượt là $a,b$ (đồng)
Theo bài ra ta có:
\(\left\{\begin{matrix} a+b=450000\\ a(1-0,25)(1+0,08)+b(1-0,4)(1+0,1)=327000\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a+b=450000\\ 0,81a+0,66b=327000\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=200000\\ b=250000\end{matrix}\right.\)