Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(α) tiếp xúc với (S) tại A
⇒ (α) ⊥ IA
⇒ (α) nhận 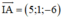 là vectơ pháp tuyến
là vectơ pháp tuyến
(α) đi qua A(6; 2; -5)
⇒ (α): 5x + y – 6z – 62 = 0.

Tâm của mặt cầu (S) là trung điểm I (1; 1; 1) của đoạn thẳng AB và bán kính của mặt cầu (S) là R = IA = √62

Chọn A
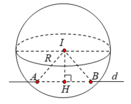
Đường thẳng d đi qua M(-5;7;0) và có vectơ chỉ phương ![]()
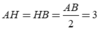
Gọi H là hình chiếu của I lên (d). Ta có:
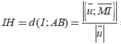
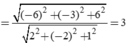
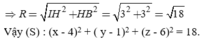

Đáp án B.
Mặt cầu (S) có tâm I(1;1;1) . Mặt phẳng (P)đi qua A và nhận I A → = ( 5 ; 1 ; - 6 ) làm vtpt
=> phương trình của (P) là: 5(x-6)+ 1(y-2) -6(z+5) = 0
<=> 5x + y – 6z - 62 = 0



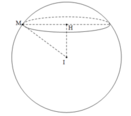



Mặt cầu (S) có phương trình là