

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Giả sử dòng điện trong đoạn mạch có chiều từ A đến B. Khi đó E 1 và E 2 đều là máy thu.
Áp dụng định luật ôm cho đoạn mạch AB ta có: I = U A B − ( E 1 + E 2 ) R + r 1 + r 2 = − 0 , 2 ( A )
Vì I < 0 nên dòng điện có chiều từ B đến A
Chọn A

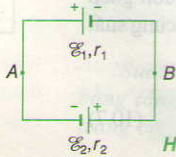
Như sơ đồ hình 10.5 thì hai nguồn điện này được mắc nối tiếp với nhau nên dòng điện chạy qua mạch kín có chiều từ dương của mỗi nguồn. Áp dụng công thức suất điện động và điện trở trong của bộ nguồn nối tiếp và đinh luật ôm đối với toàn mạch ta có cường độ dòng điện chạy trong mạch là:
I = (ξ1 + ξ2)/ (r1 + r2) = 1,5 A/
HIệu điện thế UAB trong trường hợp này là UAB = -ξ2 + Ir2 = 0.