K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

28 tháng 6 2021
ta có \(Im=Ix=\dfrac{U}{\left(Rx+r\right)}\)
\(=>Px=Ix^2.Rx=\dfrac{U^2Rx}{\left(Rx+r\right)^2}=\dfrac{U^2}{\dfrac{\left(Rx+r\right)^2}{\sqrt{Rx}^2}}\)
\(=>Px=\dfrac{U^2}{\left(\sqrt{Rx}+\dfrac{r}{\sqrt{Rx}}\right)^2}\)
Px đạt cực đại <=>\(\left(\sqrt{Rx}+\dfrac{r}{\sqrt{Rx}}\right)^2\) đạt Min
áp dụng bdt cosi(do Rx,r không âm)
\(=>\left(\sqrt{Rx}+\dfrac{r}{\sqrt{Rx}}\right)^2\ge4r\)
dấu"=" xảy ra<=>\(\sqrt{Rx}=\dfrac{r}{\sqrt{Rx}}< =>Rx=r\)
vậy Rx=r thì Px đạt cực đại
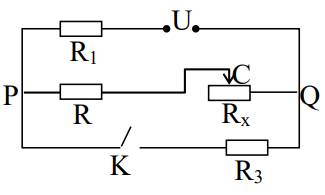



1. Khi khóa K mở, sơ đồ mạch điện như sau: R1 nt R2 nt Rx
Công suất tỏa nhiệt trên biến trở là: \(P_x=U_xI=I^2R_x=\dfrac{U^2}{\left(R_1+R_2+R_x\right)}R_x\)
\(\Leftrightarrow P_x=\dfrac{U^2}{\dfrac{R_1+R_2}{R_x}+1}\)
Để \(\left(P_x\right)_{max}\) thì \(\left(\dfrac{R_1}{R_x}+\dfrac{R_2}{R_x}\right)_{min}\)
Áp dụng BĐT Cosi vào hai số \(\dfrac{R_1}{R_x}\) và \(\dfrac{R_2}{R_x}\) ta có:
\(\dfrac{R_1}{R_x}+\dfrac{R_2}{R_x}\ge2\sqrt{\dfrac{R_1R_2}{R_x^2}}\)
Dấu "=" xảy ra khi \(\dfrac{R_1}{R_x}=\dfrac{R_2}{R_x}\)\(\Rightarrow R_2=R_1=12\Omega\)
2. Khi K đóng, sơ đồ mạch điện như sau: R1 nt [(R2 nt Rx)//R3]
Công suất tỏa nhiệt đoạn mạch PQ là: \(P=U_{23x}.I=I^2R_{23x}=\dfrac{U^2}{\left(R_1+R_{23x}\right)^2}.R_{23x}\)
\(\Leftrightarrow12=\dfrac{24^2}{\left(12+R_{23x}\right)^2}.R_{23x}\)
\(\Rightarrow R_{23x}=12\Omega\)
Ta có: \(R_{23x}=\dfrac{\left(R_2+R_x\right)R_3}{R_2+R_3+R_x}\)\(\Leftrightarrow12=\dfrac{\left(12+R_x\right).18}{12+18+R_x}\)
\(\Rightarrow R_x=24\Omega\)