Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

trước hết phải xác định được góc thì mới tính tiếp nhé.kẻ C'H vuông góc A'B' thì ta có C'H vuông góc A'B' và C'H vuông góc BB' thì C'H vuông góc với cả mp AA'B'B và góc là BC'H=60.giờ tính khoảng cách thông qua thể tích chóp MBNC'.tính diện tích MNB và d(C;MNB) là dễ nhất.ra được thể tích thì tính tiếp diện tích BNC'.rồi lắp vào công thức thể tích là ok thôi

Đặt \(\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{AC}=\overrightarrow{b},\overrightarrow{AA'}=\overrightarrow{c}\)
với \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=0\)
và \(\left|\overrightarrow{a}\right|=a,\overrightarrow{\left|b\right|}=a\sqrt{2},\left|\overrightarrow{c}\right|=a\sqrt{3}\)
khi đó
\(\overrightarrow{AB}=\overrightarrow{a}+\overrightarrow{c,}\overrightarrow{BC}=-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
Giả sử đường vuông góc chung cắt \(\overrightarrow{AB}\) tại M và cắt \(\overrightarrow{BC'}\) tại N và \(\overrightarrow{AM}=x.\overrightarrow{AB'}=x.\overrightarrow{a}+x.\overrightarrow{c},\overrightarrow{BN}=y.\overrightarrow{BC'}=-y.\overrightarrow{a}+y.\overrightarrow{b}+y.\overrightarrow{c}\)
Suy ra \(\overrightarrow{AN}=\left(1-y\right)\overrightarrow{a}+y.\overrightarrow{b}+y.\overrightarrow{c}\)
Và do đó
\(\overrightarrow{MN}=\left(1-x-y\right)\overrightarrow{a}+y.\overrightarrow{b}+\left(y-x\right)\overrightarrow{c}\)
Ta có :
\(MN\perp AB',BC'\Leftrightarrow\begin{cases}\overrightarrow{MN}.\overrightarrow{AB}=0\\\overrightarrow{MN}.\overrightarrow{BC'}=0\end{cases}\)
\(\Leftrightarrow\begin{cases}-4x+2y+1=0\\-2x+6y-1=0\end{cases}\)
Giải hệ ta thu được \(x=\frac{2}{5},y=\frac{3}{10}\)
Từ đó :
\(MN^2=\left[\left(1-x-y\right)^2+2y^2+3\left(y-x\right)^2\right].a^2=\frac{39^a}{100}\)
Suy ra \(d\left(AB';BC'\right)=\frac{a\sqrt{39}}{10}\)

Đáp án B
Gọi M là trung điểm BC
Vì các cạnh AA’ = A’B = A’C
=> Hình chiếu của A’ trên (ABC) là tâm đường tròn ngoại tiếp ∆ABC
=> A’M ⊥ (ABC)
Xét ∆A’BC, ta có A'M = a 3
Xét ∆ABC, ta có: AB = AC = a 2
Vậy ![]()
![]()
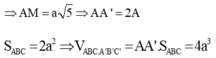
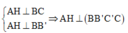
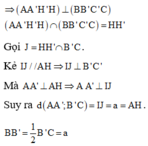
a.
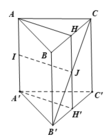
\(\left\{{}\begin{matrix}BB'\perp\left(ABC\right)\Rightarrow BB'\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ABB'A'\right)\)
\(\Rightarrow BC=d\left(C;\left(A'AB\right)\right)\)
\(S_{A'AB}=\dfrac{1}{2}S_{ABB'A'}=\dfrac{3a^2}{2}\)
\(\Rightarrow V_{C.A'AB}=\dfrac{1}{3}BC.S_{A'AB}=\dfrac{1}{3}.2a.\dfrac{3a^2}{2}=a^3\)
b.
Theo cmt, \(BC\perp\left(ABB'A'\right)\Rightarrow BC\perp AN\)
Mà \(\left\{{}\begin{matrix}A'C\perp\left(P\right)\\AN\in\left(P\right)\end{matrix}\right.\) \(\Rightarrow AN\perp A'C\)
\(\Rightarrow AN\perp\left(A'BC\right)\Rightarrow AN\perp A'B\)
c.
Ta có: \(AA'||BB'\Rightarrow d\left(B;AA'\right)=d\left(N;AA'\right)\)
\(\Rightarrow S_{A'AN}=S_{A'AB}\)
Lại có: \(CC'||BB'\Rightarrow CC'||\left(ABB'A'\right)\)
\(\Rightarrow d\left(C';\left(ABB'A'\right)\right)=d\left(M;\left(ABB'A'\right)\right)\)
\(\Rightarrow V_{A'AMN}=V_{CA'AB}=a^3\)