Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
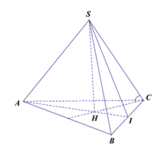
Gọi H là trọng tâm tam giác ABC, khi đó
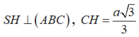
Góc giữa cạnh bên và mặt đáy là góc
![]()


Đáp án A
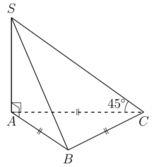
Từ giả thiết, ta suy ra góc giữa SC và mặt đáy chính là góc SCA. Suy ra tam giác SAC vuông cân ở A, và SA=AC=a.
Thể tích khối chóp là
V = 1 3 S A B C = 1 3 . 3 4 a 2 . a = 3 12 a 3

Đáp án: C.
Hướng dẫn giải:
Gọi H là tâm của tam giác ABC, M là trung điểm của AB.
Dễ dàng xác định
![]()
Đặt S H = x ⇒ H M = x ; S M = x 2
⇒ C M = 3 H M = 3 x
⇒ A B = 3 C M 3 = 2 x 3
⇒ A M = x 3
![]()
![]()
![]()
⇒ V S . A B C = S H . S A B C 3 = 15 a 3 25

Đáp án là A
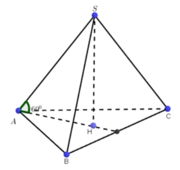
Ta có:
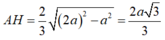
Theo giả thiết cạnh bên tạo đáy góc 60 0 suy ra góc SAH= 60 0
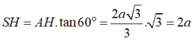
là tam giác đều cạnh 2a nên diện tích là
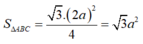
Thể tích khối chóp S.ABC là
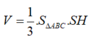
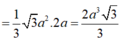

Chọn D.
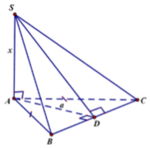
Đặt SA = x > 0. Ta có ![]() Ta có:
Ta có:
![]()
![]()
Xét tam giác vuông SBD, ta có ![]()
Khi đó: ![]()
Vậy ![]()

Đáp án: D
Hướng dẫn giả:
Gọi H là tâm của tam giác ABC
![]()
![]()
⇒ V S . A B C D = S H . S A B C 3 = 3 a 3 4 .

Đáp án B
Hướng dẫn giải:
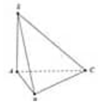
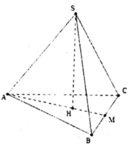
Gọi H là trọng tâm tam giác đều ABC ⇒ S H ⊥ ( A B C )
Gọi M là trung điểm của BC.
Ta có: A H = S A . cos 60 o = a 2
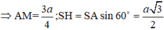
Đặt AB = x
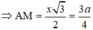
⇒ x = a 3 2
Do đó S A B C = x 2 3 4 = 3 a 2 3 16
⇒ V = 1 3 S H . S A B C = 3 a 2 32
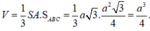
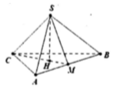
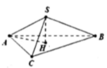
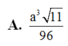
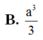
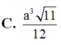
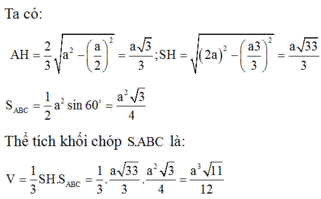
Chọn D.
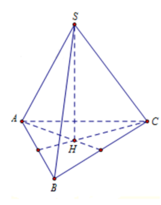
Gọi H là hình chiếu của S lên (ABC). Khối chóp S.ABC đều nên H là trọng tâm tam giác (ABC).
Xét tam giác ABI: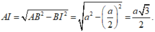
Vì H là trọng tâm tam giác ABC nên: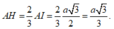
Lại có: AH là hình chiếu của SA lên (ABC)
Xét tam giác SAH: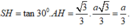
Diện tích tam giác ABC: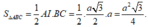
Vậy