Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn: B
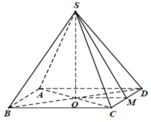
Gọi M là trung điểm củaCD, O là giao điểm của AC và BD. Ta có:


a)
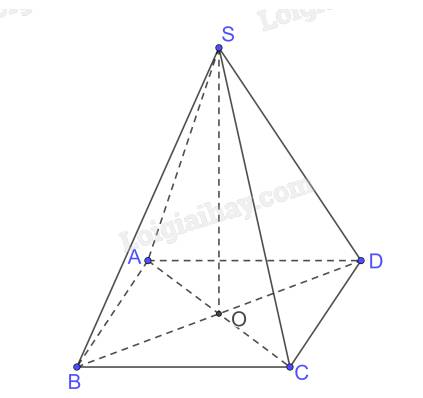
Gọi \(AC \cap BD = \left\{ O \right\}\) mà S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\)
\( \Rightarrow \) O là hình chiếu của S trên (ABCD)
C là hình chiếu của C trên (ABCD)
\( \Rightarrow \) OC là hình chiếu của SC trên (ABCD)
\( \Rightarrow \) (SC, (ABCD)) = (SC, OC) \( = \widehat {SCO}\)
Mà cạnh bên tạo với mặt đáy một góc bằng \({60^0}.\)
\( \Rightarrow \widehat {SCO} = {60^0}\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{6^2} + {6^2}} = 6\sqrt 2 \left( {cm} \right)\)
\( \Rightarrow OC = \frac{{AC}}{2} = \frac{{6\sqrt 2 }}{2} = 3\sqrt 2 \left( {cm} \right)\)
Xét tam giác SOC vuông tại O có
\(\tan \widehat {SCO} = \frac{{SO}}{{OC}} \Rightarrow SO = 6\sqrt 2 .\tan {60^0} = 6\sqrt 6 \left( {cm} \right)\)
\({S_{ABCD}} = {6^2} = 36\left( {c{m^2}} \right)\)
Vậy khối chóp có thể tích \(V = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.6\sqrt 6 .36 = 72\sqrt 6 \left( {c{m^3}} \right)\)
b)
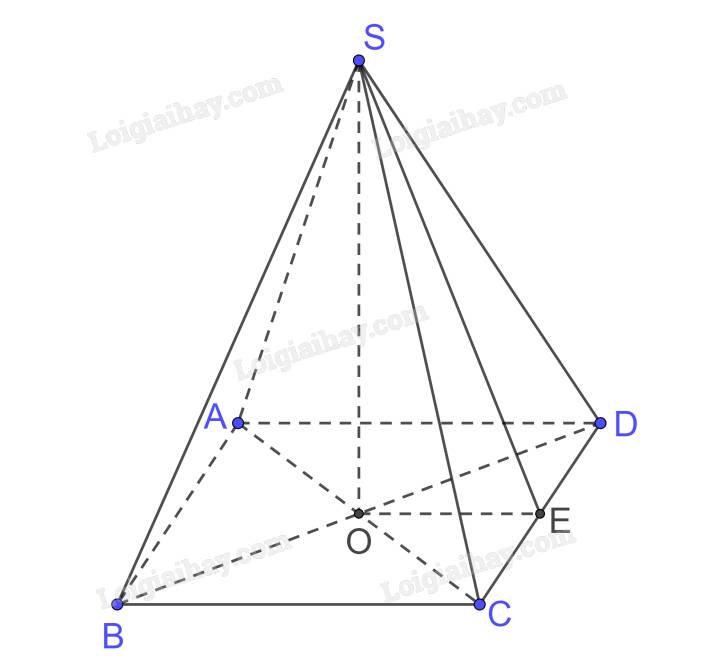
Trong (ABCD) kẻ \(OE \bot CD\)
\(\begin{array}{l}SO \bot CD\left( {SO \bot \left( {ABCD} \right)} \right)\\ \Rightarrow CD \bot \left( {SOE} \right),SE \subset \left( {SOE} \right) \Rightarrow CD \bot SE,OE \bot CD,\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\ \Rightarrow \left( {\left( {SCD} \right),\left( {ABCD} \right)} \right) = \left( {SE,OE} \right) = \widehat {SEO}\end{array}\)
Mà mặt bên tạo với mặt đáy một góc bằng \({45^0}.\)
\( \Rightarrow \widehat {SEO} = {45^0}\)
Ta có \(\left. \begin{array}{l}OE \bot CD\\AD \bot CD\end{array} \right\} \Rightarrow OE//AD\) mà O là trung điểm AC nên OE là đường trung bình tam giác ACD.
\( \Rightarrow OE = \frac{{AD}}{2} = \frac{6}{2} = 3\left( {cm} \right)\)
Xét tam giác SOE vuông tại O có
\(\tan \widehat {SEO} = \frac{{SO}}{{OE}} \Rightarrow SO = 3.\tan {45^0} = 3\left( {cm} \right)\)
Vậy khối chóp có thể tích \(V = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.3.36 = 36\left( {c{m^3}} \right)\)

Kẻ SG vuông góc (ABC)
S.ABC là khối chóp đều
=>ΔABC đều
=>G là trọng tâm, là trực tâm của ΔABC
Gọi giao của AG với BC là D
=>D là trung điểm của BC
ΔABC đều có AD là trung tuyến
nên \(AD=\dfrac{a\sqrt{3}}{2}\)
=>\(AG=\dfrac{a\sqrt{3}}{2}\cdot\dfrac{2}{3}=\dfrac{a\sqrt{3}}{3}\)
ΔSAG vuông tại G nên \(SG=\sqrt{SA^2-AG^2}=\sqrt{b^2-\dfrac{1}{3}a^2}\)
\(V_{S.ABC}=\dfrac{1}{3}\cdot S_{ABC}\cdot SG=\dfrac{1}{3}\cdot\sqrt{b^2-\dfrac{1}{3}a^2}\cdot\dfrac{a^2\sqrt{3}}{4}\)
\(=\dfrac{a^2\sqrt{3}}{12}\cdot\sqrt{\dfrac{3b^2-a^2}{3}}\)
Thể tích khối tứ diện đều có cạnh bằng a là:
\(V=\dfrac{a^2\sqrt{3}}{12}\cdot\sqrt{a^2-\dfrac{a^2}{3}}=\dfrac{a^3\sqrt{2}}{12}\)

Đáp án D.
![]()
Gọi O là tâm của hình vuông ABCD.vì S.ABCD là hình chop đều nên SO ⊥ (ABCD)
Từ giả thiết, ta có
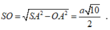
Khối nón ngoại tiếp hình chóp S.ABCD có chiều cao
![]()
và bán kính đáy là
![]()
và bán kính đáy là
Suy ra
![]()
Ta có SO là trục đường tròn ngoại tiếp hình vuông ABCD. Đường trung trực của SB nằm trong mặt phẳng (SBD) cắt SB, SO lần lượt tại M, I. Ta có IS = IB = IA = IC = ID nên I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Ta có SI.SO = SM.SB
![]()
Suy ra
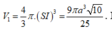
Do đó V 1 V 2 = 108 25
Phân tích phương án nhiễu.
Phương án A: Sai do HS nhớ nhầm công thức tính thể tích khối cầu là
![]()
Do đó tính được V 1 V 2 = 324 25
Phương án B: Sai do HS nhớ nhầm công thức tính thể tích khối nón là
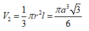
Do đó tính được V 1 V 2 = 18 30 25
Phương án C: Sai do HS nhớ sai công thức tính thể tích khối nón là
![]()
Do đó tính được V 1 V 2 = 36 25

Gọi G là trọng tâm đáy \(\Rightarrow SG\perp\left(ABC\right)\)
Gọi M là trung điểm BC \(\Rightarrow AM=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Theo tính chất trọng tâm tam giác: \(AG=\dfrac{2}{3}AM=\dfrac{a\sqrt{3}}{3}\)
Pitago tam giác vuông SAG:
\(SG=\sqrt{SA^2-AG^2}=\sqrt{b^2-\dfrac{a^2}{3}}\)
\(\Rightarrow V=\dfrac{1}{3}SG.S_{ABC}=\dfrac{1}{3}\sqrt{b^2-\dfrac{a^2}{3}}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{12}.\sqrt{b^2-\dfrac{a^2}{4}}\)

Đáp án D
Gọi O là giao AC và BD, M là trung điểm CD
Vì S.ABCD là hình chóp đều
=> O là hình chiếu của S trên (ABCD)
Ta có: OM ⊥ CD và SM ⊥ CD
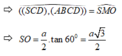
Vậy 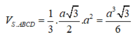


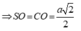
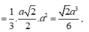
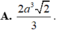
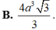
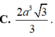
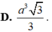



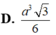

Gọi \(AC \cap BD = \left\{ O \right\}\) mà S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow OA = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác SAO vuông tại O có
\(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{2}} = \frac{{\sqrt {4{b^2} - 2{a^2}} }}{2}\)
\({S_{ABCD}} = {a^2}\)
Vậy khối chóp có thể tích \(V = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.\frac{{\sqrt {4{b^2} - 2{a^2}} }}{2}.{a^2} = \frac{{{a^2}\sqrt {4{b^2} - 2{a^2}} }}{6}\)