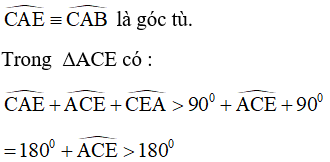Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

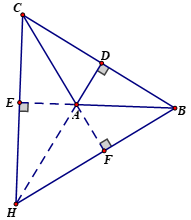
Gọi giao điểm của MB và EF là I; giao điểm của MF và AB là K.
Do ABCD là hình vuông nên AC là phân giác góc BAD. Vì thế hình chữ nhật AKME cũng là hình vuông. Từ đó suy ra MK = ME và KB = MF.
Vậy thì \(\Delta KMB=\Delta MEF\) (hai cạnh góc vuông)
Từ đó \(\widehat{MFE}=\widehat{KBM}.\)
Lại có \(\widehat{KMB}=\widehat{IMF}\) (đối đỉnh)
Vậy nên \(\widehat{IMF}+\widehat{MFI}=\widehat{KMB}+\widehat{KBM}=90^0\). hay \(\widehat{MIF}=90^0\Rightarrow MB\perp EF.\)
b. Ta chứng minh \(AF\perp EB.\) Thật vậy \(\Delta ADF=\Delta BAE\) (Hai cạnh góc vuông)
nên \(\widehat{DAF}=\widehat{ABE}\Rightarrow\widehat{ABE}+\widehat{BAF}=\widehat{DAF}+\widehat{BAF}=90^0\)
Vậy \(AF\perp EB.\). Tương tự \(EC\perp BF.\)
Xét tam giác EBF có BM; AF; CE trùng các đường cao nên chúng đồng quy.

a: Gọi giao của BM với EF là I, FM và AB là K
Vì ΔADF=ΔBAE(cạnh huyền-cạnh góc vuông)
nên góc DAF=góc ABE
=>góc ABE+góc BAF=góc DAF+góc BAF
=>góc ABE+góc BAF=90 độ
=>AF vuông góc với EB
b: Vì ABCD là hình vuông
nên AC là phân giác của góc BAD
Xét tứ giác AKME có
AK//ME
MK//AE
AM là phân giác của góc KAE
góc KAE=90 độ
Do đó: AKME là hình vuông
=>MK=ME và KB=MF
=>ΔKMB=ΔMEF
=>góc MFE=góc KBM
mà góc KMB=góc IMF
nên góc MFE+góc IMF=góc KBM+góc KMB=90 độ
=>BM vuông góc với EF
c: Xét ΔBEF có
BM,AF là các đường cao
nên BM cắt AF tại trực tâm của tam giác
=>M là trực tâm
=>BM,AF,CE đồng quy

a: Gọi giao của BM với EF là I, FM và AB là K
Vì ΔADF=ΔBAE(cạnh huyền-cạnh góc vuông)
nên góc DAF=góc ABE
=>góc ABE+góc BAF=góc DAF+góc BAF
=>góc ABE+góc BAF=90 độ
=>AF vuông góc với EB
b: Vì ABCD là hình vuông
nên AC là phân giác của góc BAD
Xét tứ giác AKME có
AK//ME
MK//AE
AM là phân giác của góc KAE
góc KAE=90 độ
Do đó: AKME là hình vuông
=>MK=ME và KB=MF
=>ΔKMB=ΔMEF
=>góc MFE=góc KBM
mà góc KMB=góc IMF
nên góc MFE+góc IMF=góc KBM+góc KMB=90 độ
=>BM vuông góc với EF
c: Xét ΔBEF có
BM,AF là các đường cao
nên BM cắt AF tại trực tâm của tam giác
=>M là trực tâm
=>BM,AF,CE đồng quy

- Trường hợp tam giác vuông:
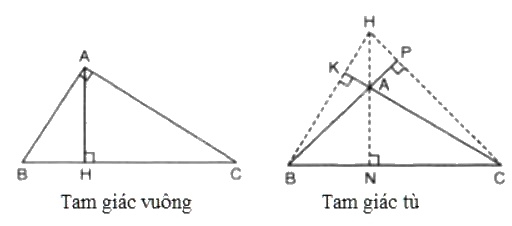
+) Xét tam giác ABC vuông tại A thì BA ⊥ CA hay A là giao điểm của hai đường vuông góc trong tam giác
⇒⇒ A trực tâm của tam giác.
Vậy trong tam giác vuông thì trực tâm trùng với đỉnh góc vuông.
+) Trường hợp tam giác tù:
Từ B kẻ đường thẳng BK vuông góc với CA.
Ta có: KA, KC lần lượt là hình chiếu của BA, BC.
Vì BC > BA nên KC > KA hay K phải nằm ngoài đoạn thẳng AC. Do đó ta có đường cao BK như hình vẽ.
Tương tự với đường cao CP.
Gọi H là giao điểm của BK và CP
⇒⇒ H chính là trực tâm của tam giác.
Ta thấy H ở bên ngoài tam giác.
Vậy trực tâm của tam giác tù nằm ở bên ngoài tam giác đó.
Cách 2:
+ Xét ΔABC vuông tại A
AB ⏊AC ⇒ AB là đường cao ứng với cạnh AC và AC là đường cao ứng với cạnh AB
hay AB, AC là hai đường cao của tam giác ABC.
Mà AB cắt AC tại A
⇒ A là trực tâm của tam giác vuông ABC.
Vậy: trực tâm của tam giác vuông trùng với đỉnh góc vuông
+ Xét ΔABC tù có góc A tù, các đường cao CE, BF (E thuộc AB, F thuộc AC), trực tâm H.
+ Giả sử E nằm giữa A và B, khi đó
Vậy E nằm ngoài A và B
⇒ tia CE nằm ngoài tia CA và tia CB ⇒ tia CE nằm bên ngoài ΔABC.
+ Tương tự ta có tia BF nằm bên ngoài ΔABC.
+ Trực tâm H là giao của BF và CE ⇒ H nằm bên ngoài ΔABC.
Vậy : trực tâm của tam giác tù nằm ở bên ngoài tam giác.
https://www.google.com/search?sxsrf=ACYBGNShkLL-JlrB5LGT8WMfh0jTHv-mgw:1581944122307&q=-Cho+tam+gi%C3%A1c+ABC+vu%C3%B4ng+c%C3%A2n+t%E1%BA%A1i+A.+G%E1%BB%8Di+I,+K+theo+th%E1%BB%A9+t%E1%BB%B1+l%C3%A0+trung+%C4%91i%E1%BB%83m+c%E1%BB%A7a+AB,+AC.+G%E1%BB%8Di+H,D+th%E1%BB%A9+t%E1%BB%B1+l%C3%A0+h%C3%ACnh+chi%E1%BA%BFu+c%E1%BB%A7a+I,A+tr%C3%AAn+BK,+M+l%C3%A0+h%C3%ACnh+chi%E1%BA%BFu+c%E1%BB%A7a+A+tr%C3%AAn+HI.+O+l%C3%A0+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+BM+v%C3%A0+AC+,P+l%C3%A0+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+AB+v%C3%A0+DM+a)+C/m+tam+gi%C3%A1c+DAK+%3D+tam+gi%C3%A1c+HBI+b)+T%C3%ADnh+s%E1%BB%91+g%C3%B3c+ADC+c)C/m+OP+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+BC&tbm=isch&source=univ&sa=X&ved=2ahUKEwi7rNuL0djnAhUKzTgGHYr8DnMQsAR6BAgDEAE&biw=1137&bih=692