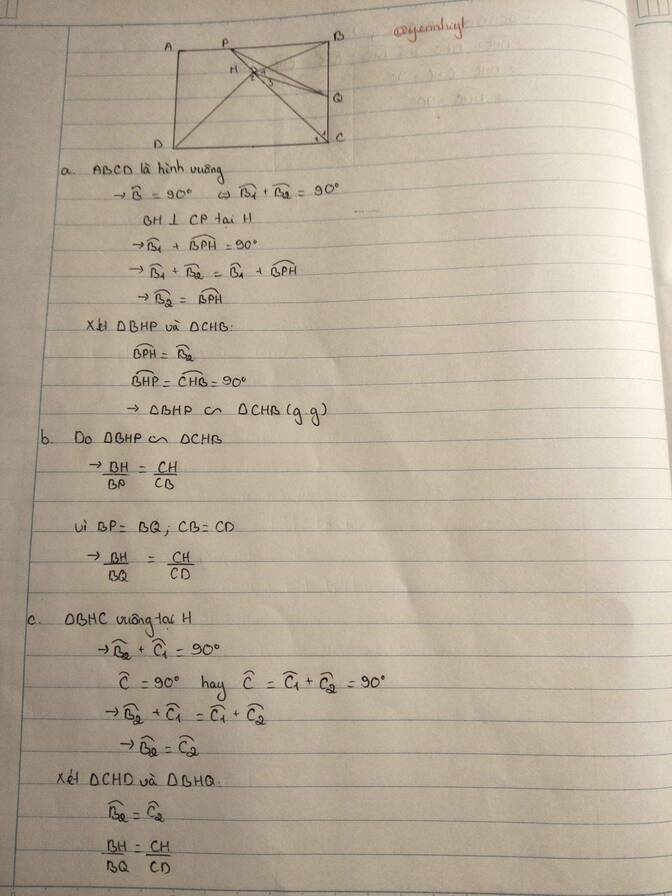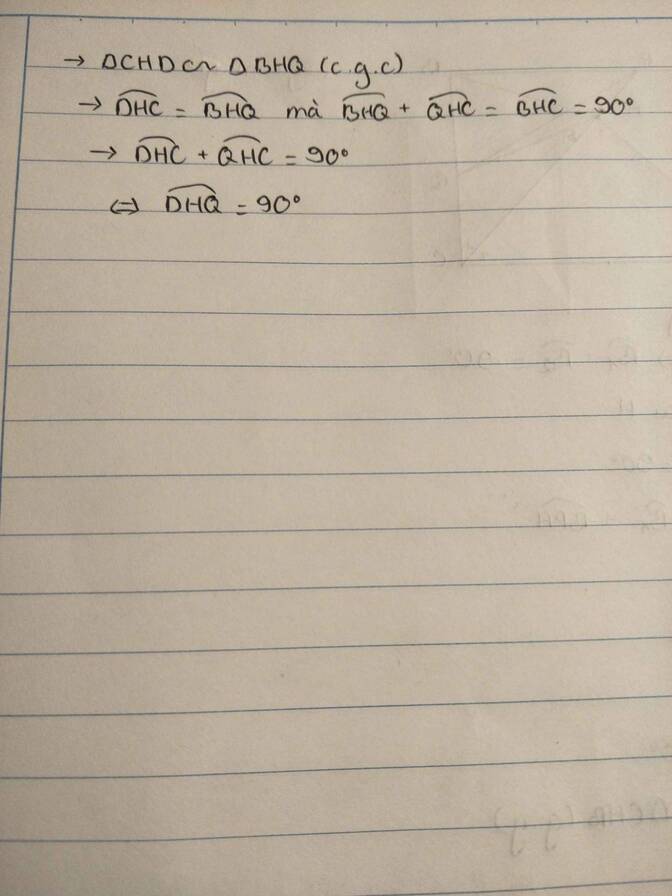Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
a , Có BH vuông góc với MC nen tam giác BHC vuông tại H suy ra góc BHC = 90 độ suy ra góc HCB + góc HBC = 90 độ
Có góc ABC = 90 độ ( hình vuông ABCD ) . Có góc MBH + góc HBC = góc ABC = 90 độ
Suy ra góc MBH = góc BCH ( cùng phụ với góc HBC )
Xét tam giác MHB và tam giác BHC có :
Góc MHB = Góc BHC ( = 90 độ )
Góc MBH = góc BCH ( c.m.t)
Suy ra tam giác MHB đồng dạng với tam giác BHC ( g.g )
Suy ra BH/HC= HM / HB hay BH/HM = HC/ BH
Suy ra BH^2 = HM . HC
Mink chứng minh tiêp câu b nha
Có BH ^2 = HM . HC
BH ^2 = 4 .9
BH ^2 = 36
BH = 6 cm
Có tam giác BHM vuông tại M
MH2 + HB2 = MB 2 ( định lý py ta go )
4^2 + 6^2 = MB^2
16 + 36 = MB ^2
MB^2 = 52
MB = Căn 52
mà MB = BN
suy ra BN = Căn 52

Cho hình vuông ABCD . Trên cạnh BA và BC lấy hai điểm P và Q sao cho BP = BQ . Kẻ BH vuông góc với PC . CM :
a) Tam giác BHP đồng dạng với tam giác CHB
b) BH/BQ=CH/CD
c) Tam giác DHC đồng dạng với tam giác QHB
d) Góc DHQ = 90O

1:
Sửa đề: ΔBEC
Xét ΔHBC vuông tại H và ΔBEC vuông tại B có
góc HCB chung
=>ΔHBC đồng dạng với ΔBEC
2: ΔHBC đồng dạng với ΔBEC
=>CH/CB=BH/BE
=>CH/CD=BH/BF

a) Gọi E là trung điểm BK
Chứng minh được QE là đường trung bình \(\Delta\)KBC nên QE//BC => QE _|_ AB (vì BC_|_AB) và \(QE=\frac{1}{2}BC=\frac{1}{2}AD\)
Chứng minh AM=QE và AM//QE => Tứ giác AMQE là hình bình hành
Chứng minh AE//NP//MQ (3)
Xét \(\Delta AQB\)có BK và QE là 2 đường cao của tam giác
=> E là trực tâm tam giác nên AE là đường cao thứ 3 của tam giác AE _|_ BQ
=> BQ _|_ NP
b) Vẽ tia Ax vuông góc với AF. Gọi giao Ax và CD là G
Chứng minh \(\widehat{GAD}=\widehat{BAP}\)(cùng phụ \(\widehat{PAD}\))
=> \(\Delta\)ADG ~ \(\Delta\)ABP (gg) => \(\frac{AP}{AG}=\frac{AB}{AD}=2\Rightarrow AG=\frac{1}{2}AP\)
Ta có \(\Delta\)AGF vuông tại A có AD _|_ GF nên AG.AF=AD.GF(=2SAGF)
=> \(AG^2\cdot AF^2=AD^2\cdot GF^2\left(1\right)\)
Ta chia cả 2 vế củ (1) cho \(AD^2\cdot AG^2\cdot AF^2\)
Mà \(AG^2+AF^2=GF^2\)(định lý Pytago)
\(\Rightarrow\frac{1}{AD^2}=\frac{1}{AG^2}+\frac{1}{AF^2}\Rightarrow\frac{1}{\left(\frac{1}{2}AB\right)^2}=\frac{1}{\left(\frac{1}{2}AP\right)^2}+\frac{1}{AF^2}\)
\(\Rightarrow\frac{4}{AB^2}=\frac{4}{AP^2}+\frac{1}{AF^2}\Rightarrow\frac{1}{AB^2}=\frac{1}{AP^2}+\frac{1}{4AF^2}\)