Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\widehat{AOt}=\widehat{BOt}=\dfrac{\widehat{AOB}}{2}=60^0:2=30^0\)(do Ot là phân giác \(\widehat{AOB}\))
Ta có: \(\widehat{AOt}=\widehat{OAx}=30^0\)
Mà 2 góc này so le trong
=> Ax//Ot(1)
Ta có: \(\widehat{BOt}+\widehat{OBy}=30^0+150^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> By//Ot(2)
Từ (1),(2) => đpcm

a: góc xOt=góc tOy=60/2=30 độ
b: góc xAm=góc xOy
=>Oy//Am
c: Xét tứ giác OACB có
OA//CB
OB//AC
OC là phân giác của góc BOA
Do đó: OACB là hình thoi
=>CO là phân giác của góc ACB

Bài 1:
Vì ∠AOC = ∠BOD (đối đỉnh)
Vì ∠AOC + ∠BOD = 140o (gt)
⇒ ∠AOC = ∠BOD = 140o/2 = 70o
Ta có: ∠AOC + ∠AOD = ∠COD (2 góc kề bù)
Thay số: 70o + ∠AOD = 180o
∠AOD = 180o - 70o
∠AOD = 110o
Vì ∠AOD = ∠BOC (đối đỉnh)
⇒ ∠BOC = 110o
Vậy ∠AOC = 70o
∠BOD = 70o
∠AOD = 110o
∠BOC = 110o

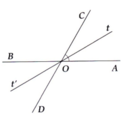
a) B O D ^ = A O C ^ = 60° (đối đỉnh.).
=> C O B ^ + A O C ^ = 180° (kề bù), => B O C ^ = 180 ° − A O C ^ = 120°
=> A O D ^ = B O C ^ = 120° (đối đỉnh),
b) Vì Ot là phân giác góc AOC nên
A O t ^ = 1 2 A O C ^ = 30°
=> B O t ' ^ = A O t ^ = 30° (đối đỉnh).
Tương tự:
D O t ' ^ = 30 ° ⇒ B O t ' ^ = D O t ' ^
Do đó Ot' là phân giác của B O D ^ .

a) Từ A kẻ A m / / b (Am nằm trong a O b ^ )
Kẻ tia Ay là tia phân giác của a A m ^ .
Ta có: a O t ^ = 1 2 a O b ^ (Ot là tia phân giác của a O b ^ )
a A y ^ = 1 2 a A m ^ (Ay là tia phân giác của a A m ^ )
Mà a O b ^ = a A m ^ (hai góc đồng vị) ⇒ a O t ^ = a A y ^
Hai góc này lại ở vị trí đồng vị nên A y / / O t
b) Vẽ tia A z ⊥ A y
Lại có A y / / O t (theo phần a)
⇒ A z ⊥ O t (Az vuông góc với một trong hai đường thẳng song song thì phải vuông góc với đường thẳng còn lại).

#)Giải :
a) Vì góc AOC và góc BOD là hai góc đối đỉnh => góc AOC = góc BOD ( = 60o)
Vì góc AOC và góc BOC là hai góc kề bù => góc BOC = 180o - góc AOC = 180o - 60o = 120o
Vì góc BOC và góc AOD là hai góc đối đỉnh => góc BOC = góc AOD ( = 120o)
b) Vì Ot là tia phân giác của góc AOC => góc AOt = góc COt = 60o/2 = 30o
Vì góc AOt và góc BOt' là hai góc đối đỉnh => góc AOt = góc BOt' ( = 30o)
Vì góc COt và góc DOt' là hai góc đối đỉnh => góc COt = góc DOt' ( = 30o)
=> góc BOt' = góc DOt' ( = 30o)
=> Ot' là tia phân giác của góc BOD
Giải
a) +) Vì \(\widehat{AOC}\)và \(\widehat{BOD}\) là 2 góc đối đỉnh
=> \(\widehat{AOC}\) = \(\widehat{BOD}\) = 60o
+) Vì \(\widehat{COB}\) và \(\widehat{BOD}\)là 2 góc kề bù
=> \(\widehat{COB}\)+ \(\widehat{BOD}\)= 180o
Hay \(\widehat{COB}\)+ 60o = 180o
\(\widehat{COB}\) = 180o - 60o = 120o
+) Vì \(\widehat{COB}\)và \(\widehat{AOD}\)là 2 góc đối đỉnh
=> \(\widehat{COB}\)= \(\widehat{AOD}\) = 120o
b) Vì Ot là tia phân giác của \(\widehat{AOC}\)
=> \(\widehat{AOt}\)= \(\widehat{tOC}\)= \(\frac{\text{}\widehat{AOC}}{2}\)= \(\frac{60^o}{2}\)= 30o
Vì \(\widehat{AOt}\)và \(\widehat{BOt'}\)là 2 góc đối đỉnh
=> \(\widehat{AOt}\)= \(\widehat{BOt'}\)= 30o
Vì \(\widehat{COt}\)và \(\widehat{DOt'}\)là 2 góc đối đỉnh
=> \(\widehat{COt}\)= \(\widehat{DOt'}\)= 30o
=> \(\widehat{BOt'}\)= \(\widehat{DOt'}\)( = 30o ) ( 1 )
Trên cùng 1 nửa mặt phẳng bờ chứa tia OD có \(\widehat{DOt'}< \widehat{DOB}\)( vì 30o < 60o )
=> Ot' nằm giữa OB và OD ( 2 )
Từ ( 1 ) và ( 2 ) => Ot' là tia phân giác của \(\widehat{BOD}\)
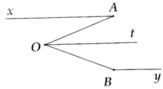
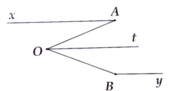

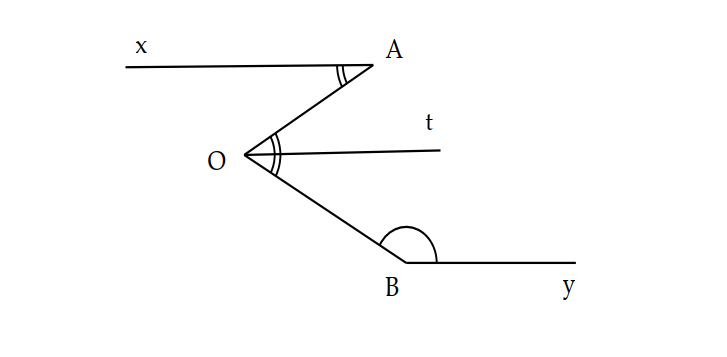


Vì Ot là phân giác A O B ^ nên:
= A O t ^ = B O t ^ = 1 2 A O B ^ = 1 2 . 60° = 30°
=> x A O ^ = A O t ^ => Ax // Ot (1)
Lại có : t O A ^ + O B y ^ = 30° +150° = 180° => Ot // By. (2)
Từ (1) và (2), ta có Ax // By // Ot