Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
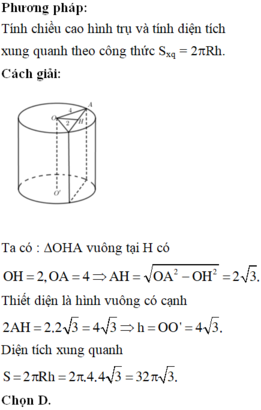
Phương pháp:
Tính chiều cao hình trụ và tính thể tích theo công thức

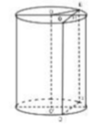

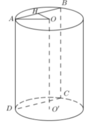
a) Theo đầu bài, hình trụ có chiều cao h = 7 cm và bán kính đáy r = 5 cm.
Vậy diện tích xung quanh bằng: Sxq= πrh = 35π (cm2)
Thể tích của khối trụ là:
V = πr2h = 175π (cm3)
b) Thiết diện là hình chữ nhật có một cạnh bằng chiều cao của hình trụ bằng 7 cm. Giả sử thiết diện là ABCD.
Ta có AD = 7 cm, OI = 3 cm.
Do tam giác OAI vuông tại A nên
AI2 = OA2 – OI2 = 25 – 9 = 16.
Vậy AI = 4 cm, AB = 8 cm.
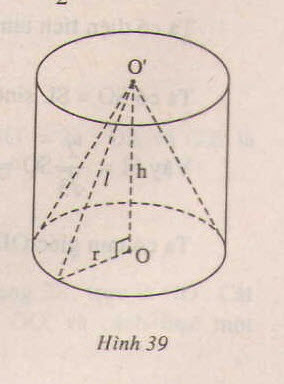

Đáp án A
Khoảng cách từ tâm đến đáy mặt phẳng cắt là 3 => Chiều rộng của hình chữ nhật là a = 2 R 2 - d 2 = 2 . 5 2 - 3 2 = 8
Vậy diện tích S của thiết diện là S = 8.7 = 56.

Đáp án A
Khoảng cách từ tâm đáy đến mặt phẳng cắt là 3
Suy ra chiều rộng của hình chữ nhật là

Đáp án D
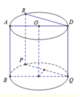
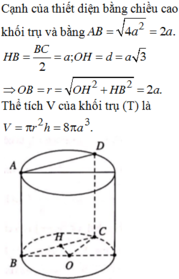
Cạnh hình vuông bằng 2 a ⇒ h T = 2 a
Bán kính đáy R = a 3 2 + 2 a 2 2 = 2 a
Suy ra V = π R 2 h = 8 π a 3


Đáp án B
Gọi hình vuông thiết diện ABCD và O là tâm đường tròn đáy của hình trụ
Gọi H là trung điểm của AB, ta có
O H = a 2 ⇒ A H = O A 2 − A H 2 = a 2 − a 2 2 = a 3 2 ⇒ A B = a 3
Chiều cao của khối trụ chính là độ dài cạnh của hình vuông bằng h = a 3
Thể tích khối trụ là V = π r 2 h = π a 3 3