Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

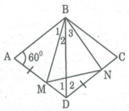
Nối BD, ta có AB = AD (gt)
Suy ra ∆ ABD cân tại A
Mà ∠ A = 60 0 ⇒ ∆ ABD đều
⇒ ∠ (ABD) = ∠ D 1 = 60 0 và BD = AB
Suy ra: BD = BC = CD
⇒ ∆ CBD đều ⇒ ∠ D 2 = 60 0
Xét ∆ BAM và ∆ BDN,ta có:
AB = BD ( chứng minh trên)
∠ A = ∠ D 2 = 60 0
AM = DN (giả thiết)
Do đó ∆ BAM = ∆ BDN ( c.g.c) ⇒ ∠ B 1 = ∠ B 3 và BM = BN
Suy ra ΔBMN cân tại B.
Mà ∠ B 2 + ∠ B 1 = ∠ (ABD) = 60 0
Suy ra: ∠ B 2 + ∠ B 3 = ∠ B 2 + ∠ B 1 = 60° hay ∠ (MBN) = 60 0
Vậy ∆ BMN đều

a: Xét ΔBAM và ΔBCN có
BA=BC
góc BAM=góc BCN
AM=CN
Do đó: ΔBAM=ΔBCN
=>BM=BN
=>ΔBMN cân tại B
b: DM+MA=DA
DN+NC=DC
mà DA=DC và MA=NC
nên DM=DN
BM=BN
DM=DN
Do đó: BD là trung trực của MN
=>BD vuông góc MN
c: Xét ΔABD có AB=AD và góc A=60 độ
nên ΔABD đều
ΔABD đều có BM là trung tuyến
nên BM là phân giác của góc ABD(1)
Xét ΔCBD có CB=CD và góc C=60 độ
nên ΔCBD đều
ΔCBD đều có BN là trung tuyến
nên BN là phân giác của góc DBC(2)
Từ (1), (2) suy ra góc MBN=1/2(góc ABD+góc CBD)
=1/2*góc ABC
=60 độ
Xét ΔBMN có BM=BN và góc MBN=60 độ
nên ΔBMN đều
=>góc BMN=60 độ

Xét ΔABD có AB=AD và góc A=60 độ
=>ΔABD đều
=>góc ABD=góc ADB=60 độ và AB=AD=BD
Xét ΔBCD có CB=CD và góc C=60 độ
nên ΔBCD đều
=>BD=CB=CD và góc CBD=góc CDB=60 độ
Xét ΔBAM và ΔBDN có
BA=BD
góc BAM=góc BDN
AM=DN
=>ΔBAM=ΔBDN
=>BM=BN và góc ABM=góc DBN
=>góc DBN+góc DBM=60 độ
=>góc MBN=60 độ
=>ΔMBN đều
https://tailieumoi.vn/cau-hoi/hinh-thoi-abcd-co-goc-a-60-do-tren-canh-ad-lay-diem-m-tren-canh-137282.html
Nhắc lần thứ nhất, không copy câu trả lời từ nguồn khác.

Bài 1:
Do E là hình chiếu của D trên AB:
=) DE\(\perp\)AB tại E
=) \(\widehat{DE\text{A}}\)=900
Do F là hình chiếu của D trên AC:
=) DF\(\perp\)AC
=) \(\widehat{DFA}\)=900
Xét tứ giác AEDF có :
\(\widehat{D\text{E}F}\)=\(\widehat{E\text{A}F}\)=\(\widehat{DFA}\) (cùng bằng 900)
=) Tứ giác AEDF là hình chữ nhật
Xét hình chữ nhật AEDF có :
AD là tia phân giác của \(\widehat{E\text{A}F}\)
=) AEDF là hình vuông

a) Ta có ^A=1/2^ABC nên ^A=60o=>t/gABD đều
=>^D1=^D2=60o
=>^ABD=^HBK=60o=>^B1=^B2
Xét t/gABH và t/gDBK ta có:
AB=BD
^B1=^B2
^A=^D2
=>t/gABD=^DBK(g-c-g)
=>AH=DK mà AD=DC nên
=>HD=KC
=>DH+DK=AD (không đổi)
=>đpcm.
b)Có BH=BK
Lại có: ^HBK=60o=>t/gHBK đều
=>HK nhỏ nhất <=> BH nhỏ nhất
<=>BH_|_AD=>H là trung điểm AD khi đó K cũng là trung điểm của DC
Áp dujnh định lý pi-ta-go ta có:BH2=AB2-AH2=22-12=3=>BH=\(\sqrt{3}\)
Vậy H và K để HK ngắn nhất: \(\sqrt{3}\)

Sửa đề: Chứng minh góc EFM = 900 ?
Có DF = CK => DF + FK = CK + FK => DK = CF. Xét \(\Delta\)EKF có ^EKF = 900
=> ME2 = KE2 + KM2 (ĐL Pytagoras). Tương tự: KE2 = DE2 + DK2 ; KM2 = CK2 + CM2
Do đó ME2 = DE2 + DK2 + CK2 + CM2. Thay CK = DF, DK = CF ta được:
ME2 = (DE2 + DF2) + (CF2 + CM2) = FE2 + FM2 (ĐL Pytagoras)
Áp dụng ĐL Pytagoras đảo vào \(\Delta\)EMF suy ra \(\Delta\)EMF vuông tại F => ^EFM = 900.
Cho mình sửa dòng thứ 2: "Xét \(\Delta\)EKM có ^EKM = 900 "
Chọn B