Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

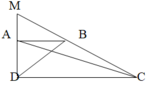
Xét tam giác ABC và ACD có cùng chiều cao chính là chiều cao hình thang, đáy dc gấp 3 đáy AB => S_ACD gấp 3 lần S_ABC.
Vậy diện tích tam giác ABC là : 16 : (3 + 1) = 4 (cm2)
Xét tam giác MAB và MAC có chung đáy MA mà CD gấp 3 lần AB (vì AB và CD cùng vuông góc với MD) => S_MAB = 1/3 S_MAC => S_MAB = 1/2 S_ABC
Vậy diện tích MAB là : 4 : (3-1) = 2 (cm2)

Nối B với D và nối A với C.
Xét 2 tam giác: BAD và CAD. Có:
-Chung đáy AD
-Chiều cao AB = 1 3 CD
=> S.BAD = 1 3 S.CAD
Do đó: S.BAD = 1 4 S.ABCD
S.BAD = 16 : 4 = 4 ( c m 2 )
S.BDC = 16 - 4 = 12 ( c m 2 )
Tam giác BDM và tam giác CDM có chung đáy MD và chiều cao BA = 1 3 CD
Do đó: S.BDM = 1 3 S.CDM
Suy ra S.BDM = 1 2 S.BDC
Mà S.BDC = 12 c m 2 . Nên S.BDM = 12 : 2 = 6 ( c m 2 )
Vì S.MAB = S.BDM - S.BAD . Nên S.MAB = 6 – 4 = 2 ( c m 2 )
Đáp số: S.MAB = 2 ( c m 2 )

Đầu tiên ta nối B với D
Ta có : \(\Delta ABD=\frac{1}{3}\Delta BDC\)vì hai tam giác có chung cao AD nhưng đáy AB = 1/3 đáy CD
\(\Delta MDB=\frac{1}{3}\Delta MDC\)vì hai tam giác có chung đáy MD và cao AB = 1/3 cao CD
Vậy \(\Delta MDC=\Delta BDC+\Delta MBD\)
\(\Delta MDC=\Delta BDC+\frac{1}{3}\Delta MDC\Leftrightarrow\Delta BDC=\frac{2}{3}\Delta MDC\)
\(\Leftrightarrow\Delta MBD=\frac{1}{2}\Delta BDC\)vì tam giác MBD = 1/3 tam giác MDC nhưng tam giác BDC = 1/3 x 2 = 2/3 tam giác MDC\
\(\Rightarrow\Delta MBD=\frac{1}{2}\Delta BDC=\frac{3}{4}\cdot\frac{1}{2}ABCD=16\cdot\frac{3}{4}\cdot\frac{1}{2}=12\cdot\frac{1}{2}=6\left(cm^2\right)\)
\(ABCD=\Delta BDC+\Delta ABD=12+4\)
Thế vào ta có :
\(\Delta MBD=\Delta ABD+\Delta MAB=4+\Delta MAB\Leftrightarrow6=4+\Delta MAB\)
\(\Rightarrow\Delta MAB=2\left(cm^2\right)\)

A B C D M
Nối A với C
Hai tam giác ABC và ADC có chiều cao hạ xuống từ đỉnh C và đỉnh A bằng nhau ( đều là chiều cao của hình thang ) mà đáy \(AB=\frac{1}{3}\)đáy \(CD\)
\(\Rightarrow S_{ABC}=\frac{1}{3}S_{ADC}\)
Vì hai tam giác AMB và AMC có chung đáy AM; chiều cao của tam giác AMB là AB còn chiều cao của tam giác AMC là CD mà \(AB=\frac{1}{3}CD\)
\(\Rightarrow S_{AMB}=\frac{1}{3}S_{AMC}\)
Do \(\frac{S_{ABC}}{S_{ADC}}=\frac{1}{3}\Rightarrow\frac{S_{ABC}}{S_{ABC}+S_{ADC}}=\frac{1}{1+3}\Leftrightarrow\frac{S_{ABC}}{S_{ABCD}}=\frac{1}{4}\)
\(\Rightarrow S_{ABC}=\frac{1}{4}.16=4\left(cm^2\right)\)
Mà \(\frac{S_{ABM}}{S_{ACM}}=\frac{1}{3}\Rightarrow\frac{S_{ABM}}{S_{ACM}-S_{ABM}}=\frac{1}{3-1}\Leftrightarrow\frac{S_{ABM}}{S_{ABC}}=\frac{1}{2}\)
\(\Rightarrow S_{ABM}=\frac{1}{2}.4=2\left(cm^2\right)\)
Vậy diện tích hình tam giác MAB là \(2cm^2.\)
( Bạn vẽ hình ra )
( Vẽ thêm hình nữa và hạ từ đỉnh B xuống đáy DC sao cho trong hình thang cuông có đủ 4 hình tam giác )
Ta có DT của cả 4 hình tam giác trng hình thang vuông ABCD đều bằng nhau vì tất cả đều có chung đáy AB và chiều cao AD .
DT hình tam giác ABD là :
16 : 4 = 4 ( cm2 )
DT BDM = 1/3 DT CDM
DT tam giác BDC là :
16 - 4 = 12 ( cm2 )
DT BDM = 1/2 DT BDC
DT tam giác BDM là :
12 : 2 = 6 ( cm2 )
DT tam giác MAB là :
6 - 4 = 2 ( cm2 )
Đáp số : 2 cm2 .
 s bn lại vt sai đề // mk hc bài này ồi
s bn lại vt sai đề // mk hc bài này ồi