NN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
0
CM
2 tháng 2 2019
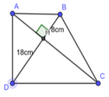
Xét ∆ ADB vuông tại A có: AH là đường cao ứng với cạnh huyền BD
⇒ A H 2 = HB. HD = 8.18 HA = 12 (cm) (hệ thức lượng trong tam giác vuông)
Xét ∆ ADC vuông tại D có: DH là đường cao ứng với cạnh huyền AC
⇒ H D 2 = H A . H C ⇒ 18 2 = 12 H C => HC = 27 (cm) (hệ thức lượng trong tam giác vuông)
Ta có: AC = AH + HC = 12 + 27 = 39 cm
BD = BH + HD = 8 + 18 = 26cm
S A B C D = A C . B D 2 = 26.39 2 = 507 c m 2
Đáp án cần chọn là: D
P
1
24 tháng 6 2021
Kẻ \(CF\perp AB\) tại F
Suy ra ADCF là hình chữ nhật (vì tứ giác có 3 góc vuông)
\(\Rightarrow\left\{{}\begin{matrix}AF=CD=30cm\\AD=FC\end{matrix}\right.\)
Có \(\widehat{FCA}=\widehat{B}=60^0\) (vì cùng phụ góc CAF)
Áp dụng hệ thức lượng vào tam giác vuông AFC:
\(FC=cot\widehat{FCA}.AF\)\(=cot60^0.30=10\sqrt{3}\left(cm\right)\)
Áp dụng ht lượng vào tam giác vuông ABC :
\(FC^2=AF.FB\)\(\Rightarrow FB=\dfrac{FC^2}{AF}=10\left(cm\right)\)
\(\Rightarrow AB=FA+FB=40\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}AD\left(AB+CD\right)=\dfrac{1}{2}CF.\left(40+30\right)=\dfrac{1}{2}.10\sqrt{3}.70\)\(=350\sqrt{3}\left(cm^2\right)\)
Vậy...
NT
0
26 tháng 9 2021
a: Xét ΔDAB vuông tại A có
\(DB^2=AB^2+AD^2\)
hay DB=25(cm)
Xét ΔDAB vuông tại A có AO là đường cao ứng với cạnh huyền DB
nên \(\left\{{}\begin{matrix}AD^2=DO\cdot DB\\AB^2=BO\cdot BD\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DO=16\left(cm\right)\\OB=9\left(cm\right)\end{matrix}\right.\)
26 tháng 9 2021
\(a,BD=\sqrt{AB^2+AD^2}=25\left(cm\right)\left(pytago\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AD^2=OD\cdot BD\\AB^2=OB\cdot BD\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}OD=\dfrac{AD^2}{BD}=16\left(cm\right)\\OB=\dfrac{AB^2}{BD}=9\left(cm\right)\end{matrix}\right.\)
\(b,\) Áp dụng HTL:
\(\left\{{}\begin{matrix}AO^2=DO\cdot OB=144\\AD^2=AO\cdot AC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AO=12\left(cm\right)\\AC=\dfrac{AD^2}{AO}=\dfrac{100}{3}\left(cm\right)\end{matrix}\right.\)
\(c,DC=\sqrt{AD^2+AC^2}=\dfrac{20\sqrt{34}}{3}\left(cm\right)\\ S_{ABCD}=\dfrac{1}{2}AD\left(AB+CD\right)=10\left(\dfrac{20\sqrt{34}}{3}+15\right)=\dfrac{450+200\sqrt{34}}{3}\left(cm^2\right)\)
DD
Đoàn Đức Hà
Giáo viên
22 tháng 6 2021
Dựng hình bình hành \(ABEC\).
Khi đó \(E\in DC\).
Vì \(BD\perp AC\)mà \(AC//BE\)nên \(BE\perp BD\).
Kẻ \(BH\perp DE\).
Xét tam giác \(BED\)vuông tại \(B\)đường cao \(BH\):
\(\frac{1}{BH^2}=\frac{1}{BD^2}+\frac{1}{BE^2}\Leftrightarrow\frac{1}{4^2}=\frac{1}{5^2}+\frac{1}{BE^2}\Leftrightarrow BE=\frac{20}{3}\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}.AC.BD=\frac{1}{2}.BD.BE=\frac{1}{2}.5.\frac{20}{3}=\frac{50}{3}\left(cm^2\right)\)