Question

[Truong Tuan MInh]

Cho hình thang MNPQ, có đáy bé MN bằng 3/5 đáy lớn PQ. Hai đường chéo MP và NQ cắt nhau tại K. Biết diện tích tam giác NPK là 15cm2. Tính diện tích hình thang MNPQ.

Answer 1

[Akai Haruma]

Lời giải:

$S_{MNQ}=S_{MNP}$ (do chiều cao bằng nhau và chung đáy)

$\Rightarrow S_{MQK}=S_{NKP}=15$ (cm²)

Kẻ đường cao $NH$ xuống $MP$, đường cao $QT$ xuông $MH$

\(\frac{S_{MNP}}{S_{MQP}}=\frac{MN}{PQ}=\frac{3}{5}\)

\(\frac{S_{MNP}}{S_{MQP}}=\frac{NH}{QT}\)

\(1=\frac{S_{NPK}}{S_{MQK}}=\frac{NH\times PK}{QT\times MK}\Rightarrow \frac{NH}{QT}=\frac{MK}{PK}\)

Từ 3 điều trên suy ra $\frac{MK}{PK}=\frac{3}{5}$

$\frac{S_{MNK}}{S_{NPK}}=\frac{MK}{PK}=\frac{3}{5}$

$S_{MNK}=\frac{3}{5}\times S_{NPK}=\frac{3}{5}\times 15=9$ (cm²)

$\frac{S_{MQK}}{S_{PQK}}=\frac{MK}{PK}=\frac{3}{5}$

$\Rightarrow S_{PQK}=\frac{5}{3}\times S_{MQK}=\frac{5}{3}\times 15=25$ (cm²)

Diện tích hình thang:

$15+15+9+25=64$ (cm²)

Answer 2

[Akai Haruma]

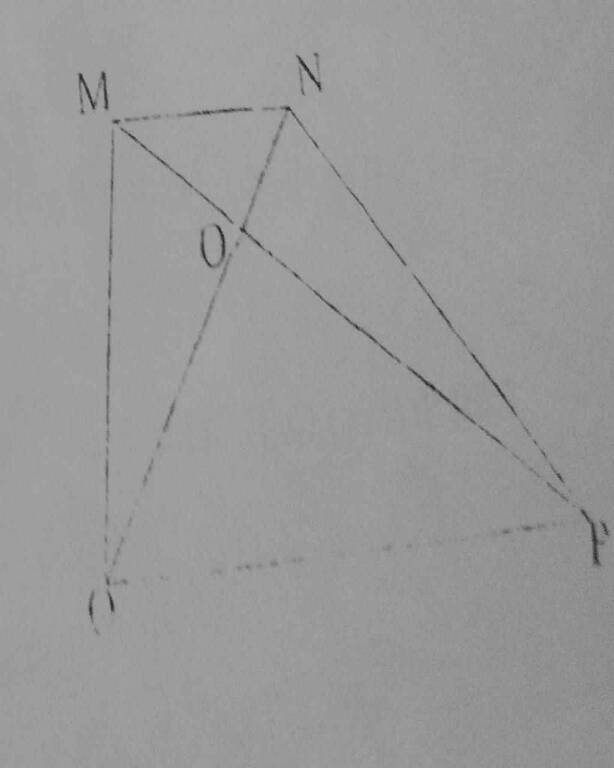
Hình vẽ: