Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB

ta có MNPQ là hình thang=>MN//PQ
mà \(=\angle\left(NMP\right)=\angle\left(MNQ\right)=>\angle\left(NQP\right)=\angle\left(MPQ\right)\)
=>tam giác MNO cân tại O=>MO=NO
=>tam giác QOP cân tại O=>OQ=Op
=>MO+OP=NO+OQ=>NQ=MP
=>MNPQ là hình thang cân
\(=>\angle\left(M\right)=\angle\left(N\right)\left(1\right)\)
\(\angle\left(Q\right)=\angle\left(P\right)\left(2\right)\)
mà EF//PQ=>EF//MN
=>MNFE là hình thang(3)
từ (1)(3)=>MNFE là hình thang cân
=>EFPQ là hình thang(4)
(2)(4)=>EFPQ là hình thang cân
Ta có: \(\widehat{OMN}=\widehat{OPQ}\)
\(\widehat{ONM}=\widehat{OQP}\)
mà \(\widehat{OMN}=\widehat{ONM}\)
nên \(\widehat{OPQ}=\widehat{OQP}\)
Xét ΔOMN có \(\widehat{OMN}=\widehat{ONM}\)
nên ΔOMN cân tại O
Xét ΔOPQ có \(\widehat{OPQ}=\widehat{OQP}\)
nên ΔOPQ cân tại O
Ta có: OM+OP=MP
ON+OQ=QN
mà OM=ON
và OP=OQ
nên MP=QN
Hình thang MNPQ có MP=QN
nên MNPQ là hình thang cân
Suy ra: \(\widehat{EMN}=\widehat{FNM}\) và \(\widehat{EQP}=\widehat{FPQ}\)
Hình thang EMNF có \(\widehat{EMN}=\widehat{FNM}\)
nên EMNF là hình thang cân
Hình thang EQPF có \(\widehat{EQP}=\widehat{FPQ}\)
nên EQPF là hình thang cân

a: Xét ΔABC có
\(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)
Do đó: MN//BC
Xét tứ giác BNMC có MN//BC
nên BNMC là hình thang
mà \(\widehat{NBC}=\widehat{MCB}\)
nên BMNC là hình thang cân

a: Xét ΔABC có
N là trung điểm của AB
M là trung điểm của AC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC
Xét tứ giác BNMC có NM//BC
nên BNMC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BNMC là hình thang cân

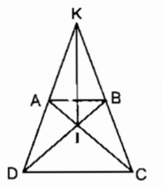
∆ ACD = ∆ BDC (c.c.c)
Suy ra 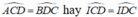
⇒ Tam giác ICD cân tại I.
do đó ID = IC (1)
Tam giác KCD có hai góc ở đáy bằng nhau ∠ C = ∠ D nên tam giác KCD cân tại K
⇒ KD = KC (2)
Từ (1) và (2) suy ra KI là đường trung trực của CD.
Chứng minh tương tự có IA = IB, KA = KB
Suy ra KI là đường trung trực của AB

Xét ΔQDC có AB//DC
nên QA/AD=QB/BC
mà AD=BC
nên QA=QB
QA+AD=QD
QB+BC=QC
mà QA=QB và AD=BC
nên QD=QC
Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
=>ΔABD=ΔBAC
=>góc DBA=góc BAC
=>góc PAB=góc PBA
=>PA=PB
PA+PC=AC
PB+PD=BD
mà PA=PB và AC=BD
nên PC=PD
PA=PB
QA=QB
=>PQ là trung trực của AB
PD=PC
QD=QC
=>PQ là trung trực của DC
a) Ta có: góc Q =góc P
=> AQ = AP ( quan hệ giữa góc và cạnh đối diện)
Ta có: AM + MQ = AQ
AN + NP = AP
Mà MQ = NP ( MNPQ là hình thang cân).
AQ = AP (cmt)
=> AM = AN => tam giác MAN cân tại A.
Câu b bạn tự làm nha