Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE và ΔKCE có
\(\widehat{ABE}=\widehat{KCE}\)
BE=CE
\(\widehat{AEB}=\widehat{KEC}\)
Do đó: ΔABE=ΔKCE

tu ve hinh nha
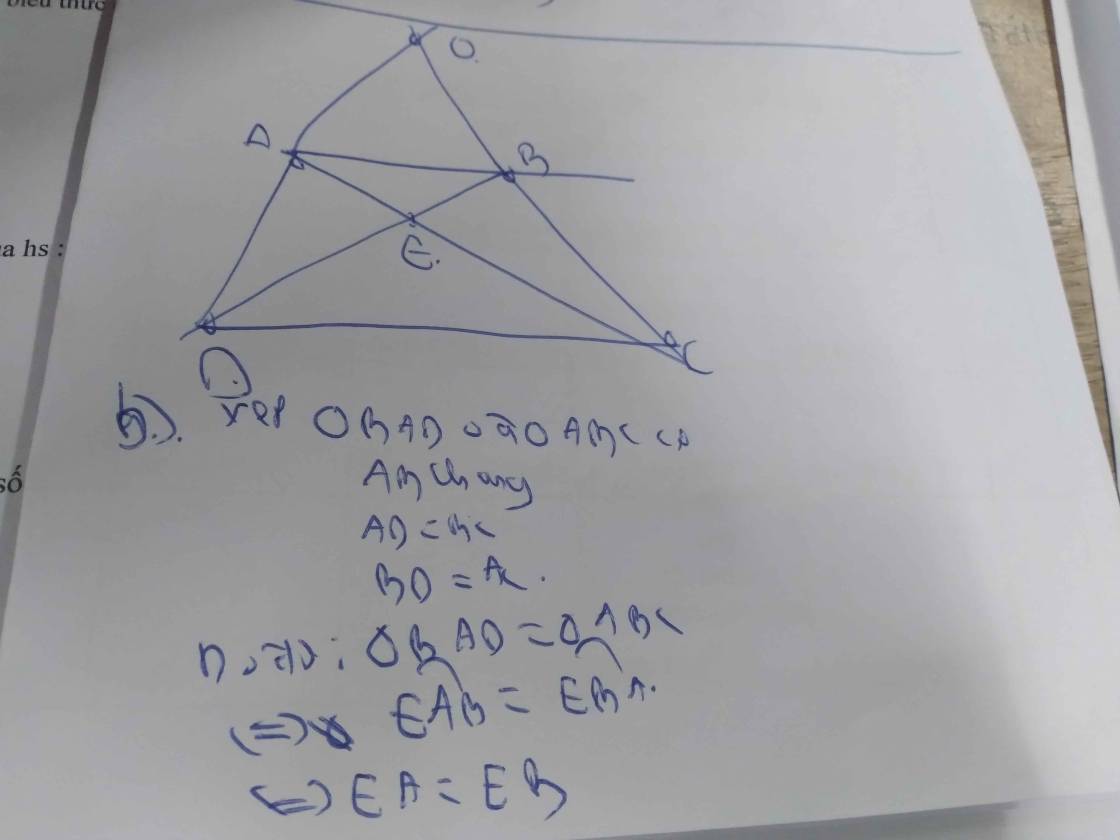
CÓ AB//CD
=> GÓC OAB = GOC ODC( 2 GÓC ĐỒNG VỊ )
VA GÓC OBS = GÓC OCD ( 2 GÓC ĐỒNG VỊ )
MÀ GÓC ODC = GÓC OCD( ABCD LÀ HÌNH THANG CÂN )
=> GÓC OAB = GÓC OBÂ
=> TAM GIAC OAB LA TAM GIÁC CÂN
B) XÉT TAM GIÁC BAD VÀ TAM GIÁC ABC CÓ :
AD=BC( ABCD LÀ HÌNH THANG CÂN )
AB CHUNG
AC=DC ( ABCD LA HINH THANG CÂN )
=> Tam giác ABD = tgiac BAC
C) CÓ TAM GIÁC ABC= TAM GIÁC BAD( CM CÂU B)
=> GÓC BAC = GÓC ABD ( 2 GÓC TƯƠNG ỨNG )
=> TAM GIÁC EAB CÂN TẠI E( CMT CÂU C)
=> AE=BE( ĐN TAM GIÁC CÂN )
CÓ AC = BD( ABCD LÀ HÌNH THANG CÂN )
MÀ AE = BE ( CMT)
=> ED=EC
D) CÓ AO =BO( TAM GIÁC AOB CÂN TẠI O)
=> O THUỘC VÀO ĐƯỜNG TRUNG TRỰC CỦA AB
CÓ EB=EB
=> E THUỘC VÀO ĐƯỜNG TRUNG TRỰC CỦA AB
=> OE THUỘC VÀO ĐG TT CỦA AB
CÓ OD=OC ( CÁI NÀY TỰ CM )
=> O THUỘC VÀO ĐG TT CỦA CD
CÓ ED=EC
=> E THUỘC VÀO ĐG TT CỦA CD
=> OE THUỘC ....... CD

a) Vì ABCD là hình thang cân
=> DAB = CBA
AD = BC
AC = BD
Ta có :
BAD + BAO = 180° ( kề bù )
CBA + ABO = 180° ( kề bù )
=> OAB = OBA
=> ∆OAB cân tại O
b) Xét ∆ABD và ∆BCA có :
AB chung
DAB = CBA (cmt)
AC = BD (cmt)
=> ∆ABD = ∆BCA (c.g.c)
c) Vì ∆ABD = ∆BCA
=> ADB = BCA
Xét ∆AED và ∆BEC có :
AD = BC
AED = BEC ( đối đỉnh )
ADB = BCD
=> ∆AED = ∆BEC (g.c.g)
=> DE = EC
d ) Vì ∆OAB cân tại O
=> OE là trung trực ∆OAB
Mà AB//CD ( ABCD là hình thang)
=> OE là trung trực CD

( Tự vẽ hình )
a) Xét \(\Delta ABE\)và \(\Delta KCE\)có :
\(\widehat{CEK}=\widehat{BEA}\)( đối đỉnh )
\(CE=EB\left(gt\right)\)
\(\widehat{KCB}=\widehat{CBA}\left(DK//AB\right)\)
\(\Rightarrow\Delta ABE=\Delta KCE\left(g-c-g\right)\left(đpcm\right)\)
b) \(\Rightarrow AE=EK\)
Xét \(\Delta ADK\)có AE = EK \(\Rightarrow DE\)là trung tuyến \(\Delta ADK\)
Mà DE là đường phân giác \(\Delta ADK\)
\(\Rightarrow\Delta ADK\)cân tại D ( đpcm )
c) \(\Rightarrow\)DE là đường cao \(\Delta ADK\)
\(\Rightarrow\widehat{AED}=90^o\left(đpcm\right)\)

Ta có:
AB song song CD <=> AB song song CK
=> Goc ABE = goc ECK so le trong
Xet hai tam giac ABE va tam giac KCE ta co:
+) Goc ABE = goc ECK
+) Canh BE = canh EC ( E la trung diem cua BC)
+) Goc AEB = goc CEK ( doi dinh)
=> Tam giac ABE = tam giac KCE (gcg)

a)xét 2 tg ABE và tg KCE có
Góc AEB=góc KEC(đ đ)
BE=EC(E là tđ BC)
Góc ABE= góc ECK(so le trong,AB//CD)
=> ABE=KCE(c.g.c)
b) ADK cân do DE vừa là đường cao vừa là đường trung tuyến(AE=EK do ABE=KCE)
C)tg AED=KED(cgv.cgv)
=>góc ADE= góc EDK
câu d mình quên công thức tính S rồi nên ko làm đc ^^
b)


Chọn D