Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì OE // DC ==> OA/AC = OE/DC (định lý Ta-let) (1)
Vì OF // DC ==> OB/BD = OF/DC (định lý Ta-let) (2)
Vì AB // CD ==> OA/OC = OB/OD (định lý ta-let)
Theo tính chất dãy tỉ số bằng nhau ta có:
OA/OC = OB/OD <=> OA / (OA + OC) = OB / (OB + OD)
<=> OA / AC = OB / BD (3)
Từ (1), (2) và (3) suy ra ta có:
OE / DC = OF / DC <=> OE = OF (đpcm)

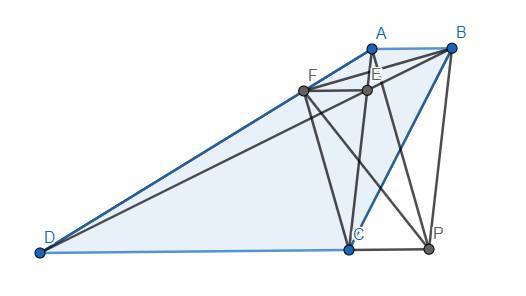
Dựng hình bình hành ABPC. Khi đó \(AD=AB+CD=CP+CD=DP\)
Ta có \(\dfrac{AB}{FE}=\dfrac{DA}{DF}\), \(\dfrac{CD}{FE}=\dfrac{DA}{AF}\)
\(\Rightarrow\dfrac{AB+CD}{FE}=DA\left(\dfrac{1}{DF}+\dfrac{1}{AF}\right)\)
\(\Rightarrow\dfrac{1}{FE}=\dfrac{DA}{DF.AF}\) \(\Rightarrow\dfrac{DF}{FE}=\dfrac{DP}{FA}\) \(\Rightarrow\dfrac{DF}{DC}=\dfrac{DP}{DA}=1\)
Từ đó \(\Delta DFC\) cân tại D. \(\Rightarrow\widehat{DFC}=\widehat{DCF}=\widehat{CFE}\) \(\Rightarrow\) FC là tia phân giác của \(\widehat{DFE}\). CMTT, FB là tia phân giác của \(\widehat{AFE}\). Do đó \(\widehat{BFC}=90^o\) (đpcm)

a: Xét tứ giác AEDF có
AE//DF
AF//DE
AD là phân giác của góc FAE
Do đó: AEDF là hình thoi
b: Xét ΔAMD vuông tại M và ΔAND vuông tại N có
AD chung
góc MAD=góc NAD
Do đó; ΔAMD=ΔAND
=>AM=AN
Xét ΔAEF có AM/AF=AN/AE
nên MN//EF

a: Xét (O) có
MB,MC là tiếp tuyến
=>MB=MC
mà OB=OC
nên OM là trung trực của BC
Xét ΔMEB và ΔMBF có
góc MBE=góc MFB
góc EMB chung
=>ΔMEB đồng dạng với ΔMBF
=>MB^2=ME*MF=MH*MO