Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì AB // CD => \(\widehat{ABD}\)= \(\widehat{ODC}\), \(\widehat{BAD}\) =\(\widehat{OCD}\)(SLT)
Nên ΔAOB ᔕ ΔCOD (g.g)
Vì AB // CD => \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}=\dfrac{4}{8}=\dfrac{1}{2}\) = OB/OD = AB/CD (ĐL Ta-lét)
=> OA.OD =OB.OC
Ta có: OA = \(\dfrac{DC}{2}\) = \(\dfrac{6}{2}\) = 3 (cm)
b, Vì AB // DM => \(\dfrac{DM}{AB}=\dfrac{MI}{AI}\) (1)
Vì AB // MI => \(\dfrac{MC}{AB}=\dfrac{MK}{AB}\)(2)
Ta có: MD = MC (3)
(1), (2) và (3) => \(\dfrac{MI}{AI}=\dfrac{MK}{KB}\)<=> IK // AB ( Định lí Ta-lét đảo)
a: Xét ΔAOB và ΔCOD có
\(\widehat{AOB}=\widehat{COD}\)
\(\widehat{OAB}=\widehat{OCD}\)
Do đó: ΔAOB\(\sim\)ΔCOD
Suy ra: \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}\)
hay \(OA\cdot OD=OB\cdot OC\)
\(\dfrac{AB}{CD}=\dfrac{OA}{OC}\)
=>\(OA=\dfrac{4}{8}\cdot6=\dfrac{1}{2}\cdot6=3\left(cm\right)\)
b:

a:
Sửa đề; EA=6cm
Xét ΔEMD và ΔEBA có
góc EMD=góc EBA
góc MED=góc BEA
=>ΔEMD đồng dạng vơi ΔEBA
=>MD/BA=ED/EA
=>10/BA=8/6=4/3
=>BA=7,5cm
b: Xét ΔFMC và ΔFBA có
góc FMC=góc FBA
góc MFC=góc BFA
=>ΔFMC đồng dạng với ΔFBA
=>FM/FB=MC/BA=MD/BA=EM/EA
=>FE//AB

a: Xét ΔIAB và ΔIMD có
góc IAB=góc IMD
góc AIB=góc MID
=>ΔIAB đồng dạng với ΔIMD
=>IA/IM=AB/MD=IB/ID
Xét ΔKAB và ΔKCM có
góc KAB=góc KCM
góc AKB=góc CKM
=>ΔKAB đồng dạng với ΔKCM
=>KA/KC=KB/KM=AB/CM
KB/KM=AB/CM
AI/IM=AB/MD
mà CM=MD
nên KB/KM=AI/IM
=>MI/IA=MK/KB
Xét ΔMAB có MI/IA=MK/KB
nên IK//AB
b: Xét ΔAMC có IK//MC
nên IK/MC=AI/AM
Xét ΔADM có EI//DM
nên EI/DM=AI/AM
Xét ΔBMC có KF//MC
nên KF/MC=BK/BM
Xét ΔMAB có IK//AB
nên AI/AM=BK/BM
=>IK/MC=FK/MC=EI/DM
mà MC=DM
nên IK=FK=EI

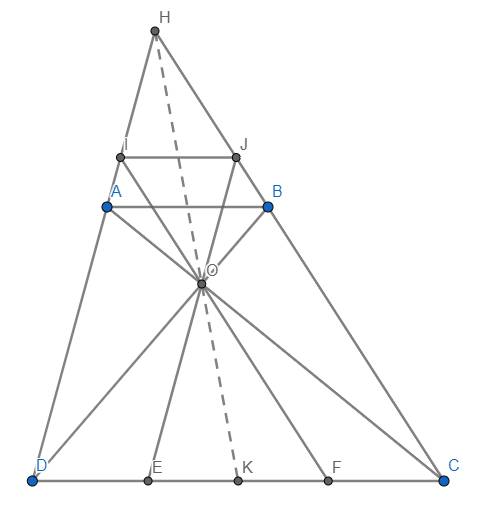
b) Theo Thales: \(\dfrac{DE}{DC}=\dfrac{AO}{AC};\dfrac{CF}{CD}=\dfrac{BO}{BD}\)
Theo câu a thì \(\dfrac{AO}{AC}=\dfrac{BO}{BD}\) \(\Rightarrow\dfrac{DE}{DC}=\dfrac{CF}{CD}\Rightarrow DE=CF\) (đpcm)
c) Từ \(DE=CF\Rightarrow\dfrac{DE}{EF}=\dfrac{CF}{EF}\)
Mà theo Thales: \(\dfrac{DE}{EF}=\dfrac{IO}{OF};\dfrac{CF}{EF}=\dfrac{JO}{OE}\)
Do đó \(\dfrac{IO}{OF}=\dfrac{JO}{OE}\) \(\Rightarrow\) IJ//CD//AB
d) Dùng định lý Menelaus đảo nhé bạn. Ta có \(\dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{OA}{OC}\) nê \(\dfrac{HA}{AD}.\dfrac{OC}{OA}=1\). Do K là trung điểm EF mà \(DE=CF\) nên K cũng là trung điểm CD hay \(\dfrac{KD}{KC}=1\). Do đó \(\dfrac{HA}{AD}.\dfrac{KD}{KC}.\dfrac{OC}{OA}=1\). Theo định lý Menalaus đảo \(\Rightarrow\)H, O, K thẳng hàng (đpcm)

a. Xét △DMI có: AB//DM.
\(\Rightarrow\dfrac{AB}{DM}=\dfrac{IA}{IM}\) (hệ quả định lí Ta-let)
a. Xét △CMK có: AB//CM.
\(\Rightarrow\dfrac{AB}{CM}=\dfrac{KB}{KM}\) (hệ quả định lí Ta-let)
Mà \(DM=CM\) (M là trung điểm DC)
\(\Rightarrow\dfrac{AB}{DM}=\dfrac{KB}{KM}\)
-Xét △ABM có: \(\dfrac{IA}{IM}=\dfrac{KB}{KM}\left(=\dfrac{AB}{DM}\right)\)
\(\Rightarrow\)IK//AB (định lí Ta-let đảo).
b) -Xét △ADM có: EI//DM.
\(\Rightarrow\dfrac{EI}{DM}=\dfrac{AI}{AM}\) (hệ quả định lí Ta-let)
-Xét △ACM có: KI//CM.
\(\Rightarrow\dfrac{IK}{CM}=\dfrac{AI}{AM}\) (hệ quả định lí Ta-let)
Mà \(DM=CM\) (M là trung điểm DC)
\(\Rightarrow\dfrac{IK}{DM}=\dfrac{AI}{AM}=\dfrac{EI}{DM}\) nên \(IK=EI\).
-Xét △BCM có: KF//CM.
\(\Rightarrow\dfrac{KF}{CM}=\dfrac{BK}{BM}\) (hệ quả định lí Ta-let)
-Xét △BDM có: IK//DM.
\(\Rightarrow\dfrac{IK}{DM}=\dfrac{BK}{BM}\) (hệ quả định lí Ta-let)
Mà \(DM=CM\) (M là trung điểm DC)
\(\Rightarrow\dfrac{IK}{CM}=\dfrac{BK}{BM}=\dfrac{KF}{CM}\) nên \(IK=KF\)
-Vậy \(EI=IK=KF\)
BMlàm sao cắt AC được bạn?